A vektor fogalma, műveletei, alkalmazása

Vektor fogalma | Vektor geometriában, lineáris algebrában, analízisben | Vektorműveletek | Vektorok alkalmazása

Mi a vektor fogalma?

Definíció: Egy irányított szakasz egyértelműen meghatároz egy vektort.

A vektoroknak van kezdőpontjuk és végpontjuk. A vektor a kezdőpontjából mutat a végpontjába.

Vektorok jelölése: . Az utolsó jelölés az A pontból B-be mutató vektort írja le.

Vektorok hosszának a jelölése: .

Az Alapok című Matek Oázis interaktív tananyagból gyorsan megtanulhatod a legfontosabbakat a vektorokról.

Mit jelent a vektor a geometriában, a lineáris algebrában és az analízis területén?

A geometriai értelmezést használjuk középiskolában. A vektorok olyan szakaszok, amiket a hosszukon kívül az irányukkal is jellemzünk.

Két vektor egyirányú, ha az őket meghatározó irányított szakaszok egyirányúak.

Két vektor ellentétes irányú, ha párhuzamosak és nem egyirányúak.

Két vektor egymás ellentettje, ha egyenlő hosszúak és ellentétes irányúak.

Két vektor egyenlő, ha irányuk és hosszuk is megegyezik.

Definíció: A nulla hosszúságú vektor neve nullvektor. A nullvektor iránya tetszőleges, minden más vektorral egyirányú. Jele: .

A lineáris algebra területén párhuzamos eltolásokat tudunk vektorokkal leírni, de ez egyetemi tananyag.

Az analízis kapcsán is egyetemi tananyagnak számítanak a vektorok.

Milyen vektorműveletek léteznek?

Vektorösszeadás

Az  és vektorok összege az a párhuzamos eltolás vektor, amivel és vektorral meghatározott párhuzamos eltolások egymásutánja helyettesíthető.

Kétféle módszerrel adhatunk össze vektorokat.

Összefűzés

Ekkor az egyik vektor  végpontjába toljuk a másik vektor  kezdőpontját. Ezután összekötjük az első vektor kezdőpontját a másik végpontjával. Ez a vektor lesz  és összege. A módszer több vektorral is működik.

Paralelogramma-szabály

A két vektort közös kezdőpontba toljuk. Ezután a vektorok végpontjain keresztülmenő párhuzamosokat húzunk a másik vektorral. Így keletkezik egy paralelogramma. A két vektor összege a közös kezdőpontból kiinduló átló.

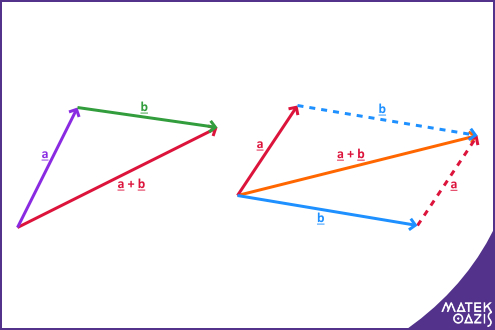
Vektorok összeadása összefűzéssel és paralelogramma-szabállyal

Vektorok különbsége

Az  és vektorok különbségét az összeadás segítségével értelmezzük: 

A két vektort közös kezdőpontba toljuk. Ezután összekötjük a kivonandó  végpontját a kisebbítendő  végpontjával.

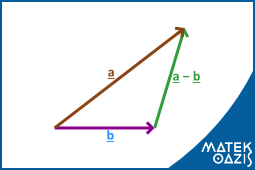
Két vektor különbsége

A Vektorok összeadása és kivonása Matek Oázis szócikkben olvashatsz bővebben erről a két műveletről, és kidolgozott feladatokat is mutatunk.

Vektor szorzása számmal

Legyen  vektor és  (lambda) valós szám. Ha egy vektort megszorzunk egy valós számmal (skalárral), akkor a vektor hossza  -szorosára változik. Ha  pozitív, akkor a vektor iránya nem változik, ha  negatív, akkor a vektor iránya az ellenkezőjére változik.

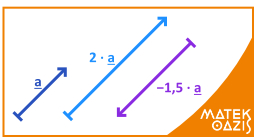
Vektor szorzása számmal

Még több feladatot oldanál meg? Kattints ide.

Vektorok skaláris szorzata

Legyen adott két vektor:  és  . A két vektor skaláris szorzata: 

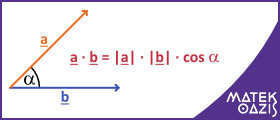
Két vektor skaláris szorzata

Az  és vektorok skaláris szorzatát ki lehet számolni a koordinátákból is:

A Vektorok című Matek Oázis tananyagban rengeteg interaktív példán keresztül gyakorolhatod a vektorműveleteket.

Hogyan alkalmazzák a vektorokat a matematikában, fizikában, számítástechnikában?

Középiskolában matematikaórán a koordinátageometria témakörben találkozunk vektorokkal. Helyvektorok segítségével végzünk el vektorműveleteket. Vektorok segítségével adjuk meg két pont távolságát.

Szakaszok felezőpontját, harmadolópontját, p:q arányú osztópontját is vektorok koordinátáinak a segítségével tudjuk megadni. Ezenkívül egyenesek egyenletét is normálvektorral, vagy irányvektorral tudjuk felírni.

Két pont távolságát is vektorok segítségével tudjuk kiszámolni koordinátageometriában. Erről bővebben a Vektor hossza, két pont távolsága Matek Oázis szócikkben olvashatsz, ahol kidolgozott feladatot is találsz. 

Fizikában sokat számolunk vektormennyiségekkel. Vektormennyiségnek számítanak azok a mennyiségek, amiknek van irányuk és nagyságuk. Ilyen például a sebesség, gyorsulás, erő, lendület, elektromos térerősség stb.

Számítástechnikában a vektorok fogalma programozás során jelenik meg. Kulcs-érték párok tárolására használják (ez hasonló az x - y párokhoz), két értéket tartanak össze, amik a hivatkozást segítik.

Egy konkrét példa: a Matek Oázisban tároljuk azt az adatot, hogy egy felhasználónak, hány csillaga van. A kulcs a felhasználó azonosítója (ID), az érték pedig a csillagok darabszáma. Alkalmazáskor lekérem, hogy például a 325-ös felhasználónak hány csillaga van, és a program kiadja, hogy 4.

Dancsó Imre
Matek- és fizikatanár