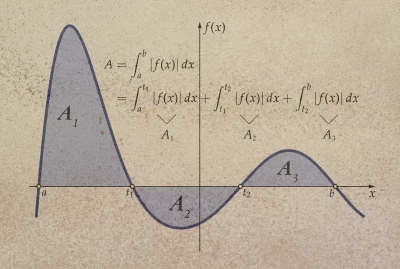Emelt matematika 11. osztály
Gyors és sikeres felkészülés a 11.-es emelt szintű matekból
Trigonometria
1. Hegyesszögek szögfüggvényei
2. NAT 2020-as kiegészítés középszinthez
3. Szögfüggvények általánosítása
4. Szinusz- és koszinusz-tétel
5. Trigonometrikus egyenletek, egyenlőtlenségek
Számelmélet, számrendszerek
6. Oszthatóság, lnko, lkkt, számrendszerek
Exp. és logaritm.
7. Hatvány, gyök
8. Exponenciális egyenletek, exp.-log. függvények
9. Logaritmus, logaritmikus egyenletek
10. Exp. és log. egyenlőtlenségek, gyakorlás
Egyenletrendszerek
11. Egyenletrendszerek megoldása
Koordinátageometria
12. Alapok
13. Egyenes normálvektoros egyenlete
14. Egyenes egyenlete meredekséggel (NAT 2020 kieg.)
15. A kör egyenlete
16. Emelt szint, parabola egyenlete
17. Gyakorlás
Kombinatorika, gráfok, valószínűség
18. Kombinatorika, gráfok
19. Valószínűségszámítás
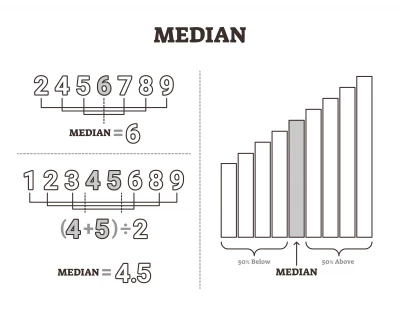
Statisztika
20. Alapfogalmak, grafikonok értelmezése, készítése
Analízis
21. Sorozatok határértéke
22. Függvények határértéke, folytonossága
23. Függvények deriválása
24. Függvényvizsgálat
25. Az integrálszámítás alapjai
26. Parciális integrálás és alkalmazások
Évvégi ismétlő/ próba pótvizsga feladatsorok
27. Ismétlés
Nem találod amit keresel?

Ha dolgozatra készülsz, jobb segítséget nem is találhatnál: egy-egy témakört rendkívül gyorsan és eredményesen tudsz átismételni úgy, hogy közben "bemászik a fejedbe" a matektudás.
Egyszerű, érthető, vidám matek :) Erőlködés és görcsök nélkül tanulhatod a matekot, és végre mindent érteni fogsz! Mindezt úgy, hogy még unalmas sem lesz a matektanulás. Világosan elmagyarázunk mindent, közben már gyakorolhatsz is, és folyamatosan ellenőrizheted magad. Próbáld ki! B. Békési Bea
A szerethető matektanulás szakértője
Matektanár

Nagyon sokat köszönhetek a matekmindenkinek.hu oldal szerkesztőinek! 11-es vagyok és ugye ez már az egyetemi felvételinél beleszámít. Az utolsó 2 dolgozatomat sikerült négyesre megírnom (2 témazáró), ezért év végén is remélhetőleg meg lesz a négyes. A videók nagyon igényesen vannak összeállítva többféle szempontból is, könnyen kezelhetőek, remek gyakorlási lehetőséget biztosítanak 1-1 dolgozat előtt. Szóval köszönöm szépen a segítséget! ;)
Erika
Soha nem gondoltam volna, hogy a matekot élvezni is lehet. Nagyon jó eredményeket értem el, mióta használom az oktató csomagot, ráadásul a fiam, aki szintén 11. osztályos, de ő természetesen nappalin jár, ő is sokkal jobb jegyeket hoz matekból, amióta velem együtt készül az órákra. Egyszóval: fantasztikus!
Balka Szilvia
...nagyon jók a videók, értem is őket, ami csak itt fordult elő nálatok.
Tarkó MelindaSzeretnéd, ha gyermeked nem csak a matekban, hanem az élet minden területén sikeresebb lenne?
LOGIKA kurzusunk játékos és interaktív módon segít gyermekednek fejleszteni a kritikus gondolkodását és a problémamegoldó képességét, amelyek egy életre szóló előnyt jelentenek.