Belső szögfelezők metszéspontjára vonatkozó tétel bizonyítása

Mi az a szögfelező? | Szögfelezőkre vonatkozó tétel | A tétel bizonyítása |Szögfelező egyenes és a háromszög beírt köre | Középszintű bizonyítások

2024-től a középszintű érettségi követelményekben szerepel néhány könnyebb bizonyítás. Nézzük most a szögfelezők metszéspontjára vonatkozó bizonyítást.

A tételt, a bizonyítást és minden fontos infót lejjebb találsz. Ha inkább meghallgatnád lépésről lépésre a bizonyítást, akkor viszont nézd meg ezt a Matek Oázis tananyagot:

Kattints a lejátszáshoz!

Próbáld ki elfektetve a telefont.

0

0:00

Feliratkozom

A szögfelező definíciója

A tétel kimondása előtt megnézzük a szögfelező definícióját, illetve egy fontos tulajdonságát.

A szögfelező a szöget két EGYENLŐ részre osztja.

A szögfelező minden pontja azonos távolságra van a szög száraitól.

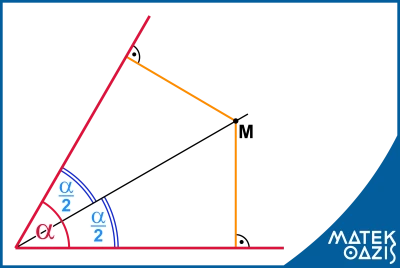
Az ábrán az 𝛼 szöghöz húztunk be egy szögfelezőt, ami két ugyanakkora, 𝛼/2 nagyságú szögre bontotta az eredeti szöget. Ahogy írtuk a szögfelező bármelyik pontja, például a kiemelt M pont egyenlő távolságra van a száraktól. (Pont és egyenes távolsága a pontból az egyenesre bocsátott merőleges szakasz hossza.)

Belső szögfelezők metszéspontjára vonatkozó tétel

A bizonyítandó tétel:

A háromszög három belső szögfelezője egy pontban metszi egymást.

A tétel bizonyítása

1. lépés: Rajzoljunk egy teljesen általános háromszöget. Behúzzuk két szögfelezőjét, e-t és f-et. Ezek metszéspontját jelöljük M-el. 

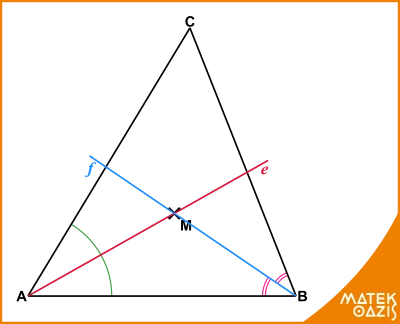
2. lépés: Mivel az M pont rajta van az e szögfelezőn, ezért kijelenthetjük, hogy az M pont egyenlő távolságra van a háromszög AC és BC oldalától, hiszen a szögfelező minden pontja egyenlő távolságra van  szögszáraktól, amik a mi esetünkben a háromszög oldalai.

Ezt a matematikában úgy jelöljük, hogy d (M ; AC) = d (M ; AB).  Ez azt jelenti tehát, hogy M pont távolsága (d : distance - távolság angolul) AC és BC oldaltól ugyanakkora. Mivel az M pont rajta van az f szögfelezőn is, ezért: d (M ; BC) = d (M ; AB).

3. lépés: összenézzük a két egyenlőséget, amit felírtunk: 

d (M ; AC) = d (M ; AB)
d (M ; BC) = d (M ; AB)​​​​​​​

M és AC távolsága éppen ugyanakkora, mint M és BC távolsága (mindkettő M és AB távolságával egyenlő). Tehát fennáll a d (M ; AC) = d (M ; BC). Ez viszont azt jelenti, hogy az M pont rajta van a háromszög harmadik szögfelezőjén is, ami a C csúcsból indul. Hiszen M egyenlő távolságra van az AC és BC oldalaktól, ezzel a tulajdonsággal pedig éppen a szögfelezői pontjai rendelkeznek.

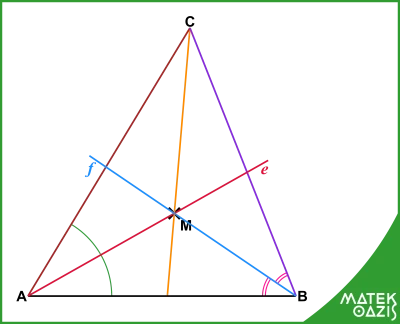
Ezzel kész a bizonyítás: a háromszög három belső szögfelezője egy pontban metszik egymást, ez az M​​​​​​​ pont. 

A háromszög beírt köre

Ahogy a bizonyításban beláttuk a három szögfelező az M pontban metszi egymást. 
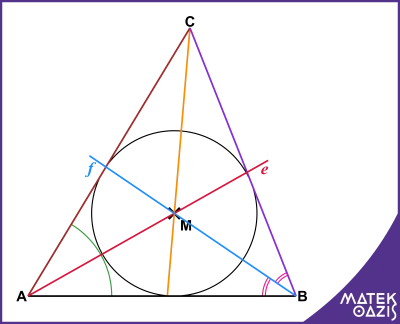
Beláttuk azt is, hogy: d (M ; AC) = d (M ; AB) = d (M ; BC). Tehát a szögfelező egyenesek M metszéspontja ugyanolyan távolságra van a háromszög mindhárom oldalától. 

Tehát az ​​​​​​​M egy olyan körnek a középpontja, ami érinti a háromszög mindhárom oldalát, és aminek sugara pedig éppen az M pont és az oldalak távolsága (d (M ; AC) = d (M ; AB) = d (M ; BC) ).

Ezt a kört hívjuk a háromszög beírt körének.

Középszintű bizonyítások

Pitagorasz-tétel bizonyítása: Matek Oázis tananyag
Pitagorasz-tétel bizonyítása: Matek Oázis cikk

Szinusztétel bizonyítása: Matek Oázis tananyag
​​​​​​​Szinusztétel bizonyítása: Matek Oázis cikk​​

Thálesz-tétel bizonyítása: Matek Oázis tananyag
​​​​​​​Thálesz-tétel bizonyítása: Matek Oázis cikk

Oldalfelezők merőlegesek metszéspontjára vonatkozó tétel bizonyítása: Matek Oázis tananyag
​​Oldalfelezők merőlegesek metszéspontjára vonatkozó tétel bizonyítása: Matek Oázis cikk

Dancsó Imre
Matek- és fizikatanár