Henger térfogata és felszíne: képletek, feladatok
Dancsó Imre,
2023. március 14.
Henger definíció | Hengertípusok | Henger térfogat képlete | Henger felszín képlete | Henger térfogata: feladat megoldással | Henger felszíne: feladatok megoldással Henger a mindennapi életben
A hengerrel már általános iskolában találkozunk. Felvételi feladatsorokban és érettségi feladatokban egyaránt megjelenik a henger felszíne és térfogata. Nézzük meg részletesen, mit kell tudni erről a testről!
Ebben a mini tananyagban összeszedtük az alapokat röviden.
Kattints a lejátszáshoz!
Kattints a lejátszáshoz!
Mi az a henger?
Ha veszünk egy körlapot, és ezt a körlapot önmagával párhuzamosan eltoljuk, akkor egy hengert kapunk.
A pontos matematikai definíció így szól: vegyünk egy síkidomot, és minden pontjába állítsunk egyenlő hosszúságú, egymással párhuzamos szakaszokat. A szakaszok végpontjai egy olyan síkidomot határoznak meg, amely egybevágó az eredeti síkidommal.
Az egybevágó síkidomokat a henger alapjainak nevezzük. (A henger alapja tehát nem csak kör lehet.)
A szakaszok neve alkotó.
A henger palástja az alkotók által meghatározott felület.
Az alapok és alkotók által meghatározott felületet nevezzük hengernek.
.jpg)
A Henger I. című Matek Oázis interaktív tananyagban minden fontos dolgot megtanulhatsz a hengerről.
Heti TOP videók INGYENES tananyagok KÓDOLATLAN hétvégék Tanulási TIPPEK KÜLÖNLEGES ajánlatok
380 ingyenes tananyag!
Milyen típusú hengerek léteznek? Hogyan származtatjuk a hengert?
A hengereket tudjuk csoportosítani aszerint, hogy az alapjuk milyen síkidom.
Amikor hengerről beszélünk, akkor szinte mindig a körhengerre gondolunk, aminek az alapja kör.
Ha a henger alapja egy sokszög, akkor hasábnak hívjuk.
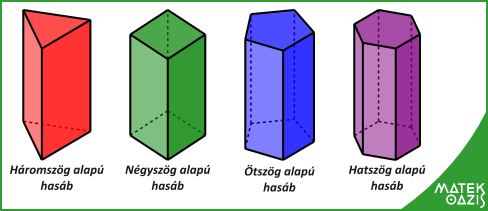
Sokszög alapú egyenes hasábok
A hengereket aszerint is tudjuk csoportosítani, hogy egyenesek-e vagy ferdék.
Azt a hengert nevezzük egyenes hengernek, amelynek alkotói merőlegesek az alapra.
Ha az alkotók nem merőlegesek az alapokra, akkor ferde hengerről beszélünk.
.jpg)
Henger térfogata: hogyan számoljuk ki?
A henger térfogatát úgy számoljuk, hogy az alapterületét megszorozzuk a magasságával:
Körhenger esetén az alap kör, ezért: 
Ezekben a képletekben a magasság a két alap síkjának távolságát jelenti. Ez egyenes körhenger esetén megegyezik az alkotó hosszával. Ferde henger esetén kicsit körülményesebb a magasság meghatározása.
Gyakorolj interaktív feladatokkal a Henger II. című Matek Oázis tananyaggal.
Henger felszíne: hogyan kell kiszámolni?
A henger felszínéhez ismernünk kell az alapjának és a palástjának a területét.
Körhenger esetén az alap kör. A palást pedig egy olyan téglalap, aminek az egyik oldala az alapkör kerülete, a másik oldala pedig az alkotó (a) hossza. Így a felszín képlet:
Henger térfogatszámítás: feladat megoldással
1. feladat: Mekkora a térfogata annak az egyenes körhengernek, amely alapkörének sugara 10 cm, alkotója 20 cm?
Megoldás: Az alap egy kör, ennek a területe: 
Mivel egyenes körhengerről van szó, ezért az alkotó megegyezik a magassággal, azaz 
, így:
Henger felszínszámítás: feladatok megoldással
2. feladat: Egy körhenger alapkörének átmérője 14 cm, magassága 25 cm. Mekkora a henger felszíne?
Megoldás: Kiszámoljuk az alapkör területét, ehhez vesszük az átmérő felét, a sugarat: 
, így a terület: 
A palást egy téglalap, aminek az egyik oldala a magasság, ami 25 cm, a másik pedig az alapkör kerülete. Kiszámoljuk ezt a kerületet: 
Így a palást területe: 
Tudunk minden adatot, behelyettesítünk a képletbe: 
3. feladat: Mennyi annak a hengernek a felszíne, aminek a palástja egy olyan téglalap, aminek az egyik oldala 25,12 cm, a másik pedig 17 cm?
Megoldás: A feladatnak 2 megoldása van. Tudjuk, hogy a palást egyik oldala az alapkör kerülete, a másik pedig a henger magassága.
Az első megoldásban legyen az alapkör kerülete 25,12 cm, a henger magassága pedig 17 cm.
Az alapkör kerületéből ki tudjuk számolni a sugarat, hiszen
→
Ismerjük a sugarat, ki tudjuk számolni az alapterületet:
A palást egy téglalap, ennek a területe a két oldalának szorzata:
Így már minden adatot ismerünk, be tudunk helyettesíteni a képletbe:
A másik megoldásban az alapkör kerülete a 17 cm a henger magassága pedig 25,12 cm.
Ugyanúgy meghatározzuk az alapkör sugarát ebben az esetben is:
Ekkor az alapterület:
A palást területe ugyanannyi, mint az első megoldásban, így a felszín:
Henger térfogatának számítása a gyakorlatban: mikor jön jól, ha tudjuk hogyan kell?
A hétköznapi életünkben körül vesznek minket a henger alakú tárgyak. Otthonunkban találhatunk henger alakú vázát, poharat, mérőedényt, befőttesüveget. Ha csak egy vonalzónk van, akkor is ki tudjuk számolni, hogy mennyi a pohár vagy üveg térfogata, és tudjuk, hogy mennyi folyadék fér bele.
A legtöbb konzervdoboz is henger alakú. Ezenkívül a benzinszállító tartálya is egy hatalmas henger. Ha tudjuk ennek a tartálynak a paramétereit, akkor meg tudjuk határozni, hogy mennyi üzemanyag szállítható benne. Aszfaltozás során úthengerrel egyengetik a készülő utat.
Festés során a szakemberek eszköze a festőhenger.
A Henger felszíne, térfogata című Matek Oázis teszttel ellenőrizheted, hogy mindent tudsz-e a hengerekről.
Matek- és fizikatanár
Mi az egészrész fogalma? Mi a törtrész fogalma? Mit kell tudni az egészrész függvényről? Mit kell tudni a törtrész függvényről?
Egészrész és törtrész függvény: definíció, feladatok
2024. május 27.
