Háromszög külső szögeinek összege

Belső szögek összege | Külső szögek összege | Összefüggés a belső és külső szögek között | Feladatok

A következő kérdést egy kedves diákunk küldte nekünk. Nézzük meg részletesen is!

Kérdés:

Mennyi a háromszög külső és belső szögeinek az összege?

Válasz (röviden):

Mivel minden külső szög 180°-ra egészíti ki a mellette fekvő belső szöget, ezért az egy csúcsnál levő külső és belső szög összege 180°. Így a 3 csúcsnál levő szögek összege 3 ∙ 180° = 540°.
De persze ugyanez jön ki akkor is, ha egyenként összeadjuk alfa, béta, gamma külső szögeit: (180° - α) + (180° - β) + (180° - γ), majd hozzáadjuk a belső szögeket: (α + β + γ). Ekkor is csak a 3×180°-ot kapunk.

Válasz részletesebben:

Mivel a külső szögekkel ritkán számolunk, ezért sokak számára nehéz ez a kérdés. Emiatt nézzük meg ezt most részletesebben is.

Mennyi a háromszög belső szögeinek összege?

7. osztályban rántjuk le a leplet erről az összefüggésről:

Tétel: Minden háromszög belső szögeinek összege 180°.

A három szöget szinte mindig a görög abc első három betűjével jelöljük. Ezek a következők: α (alfa),  β (béta), γ (gamma). A leírt tételt nagyon könnyen lehet bizonyítani váltószögek segítségével. A Háromszög szögei, oldalai című tananyagunkban megmutatjuk ezt a bizonyítást, és még sok érdekességet a háromszögekről.

Mennyi a háromszög külső szögeinek összege?

Mielőtt kimondjuk a tételt, tisztázzuk, mit nevezünk a háromszög külső szögének. Az ABC háromszögünk minden oldalát hosszabítsuk meg: az AB oldalt a B csúcson keresztül, a BC oldalt a C csúcson keresztül, és az AC oldalt az A csúcson keresztül!  Így már látjuk is a külső szögeket:  α' (alfa-vessző),  β' (béta-vessző), γ'(gamma-vessző). A külső szög mindig 180°-ra egészíti ki a mellette fekvő belső szöget.

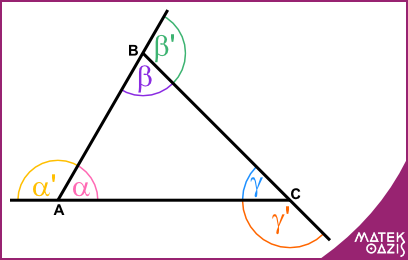
Ahogy ezen az ábrán is látszik α + α' = 180°, β + β' = 180° és γ + γ' = 180°.  Ebből mindjárt látjuk, hogy a belső és külső szögek összege  együtt (α + α' + β + β' + γ + γ' ) =  3 ∙ 180°, ami 540°. És mivel a belső szögek összege 180°, ezért:

Tétel: Minden háromszög külső szögeinek összege 360°.

A híres gízai piramisok oldallapjai háromszög alakúak

Milyen összefüggések vannak a háromszög külső és belső szögei között?

Az előbb már láttuk, hogy a háromszög belső szögeinek összege α  + β + γ = 180°. Tovább azt is láttuk, hogy hogy α + α' = 180°. Alaposan megnézve ezt a két összefüggést azt látjuk, hogy α-hoz akár α'-t, akár (β + γ)-t adunk hozzá, az összeg 180° lesz. Emiatt fennáll, hogy  α' = β + γ. Hasonlóan levezetve a másik két szögre azt kapjuk, hogy  β' = α + γ és   γ' =  α + β. Általánosságban tehát elmondhatjuk, hogy

A háromszögben egy külső szög egyenlő a nem mellette fekvő  két belső szög összegével.

Feladatok a háromszögek szögeivel kapcsolatban

1. Feladat: Mekkorák annak a háromszögnek a külső szögei, amelynek két belső szöge: α = 39°, β = 67°?

Megoldás: Először érdemes kiszámolni a harmadik belső szöget is. γ = 180°- (α + β) = 180°- (39° + 67°) 180° - 106° = 74°.
Ahogy írtuk, a háromszög egy belső szögének és a hozzátartozó külső szögének az összege 180°. Tehát: 

α + α' = 180° ➡ α' = 180° - α = 180° - 39° = 141°
β + β' = 180° ➡ β'  = 180° - β = 180° - 67° = 113°
γ  + γ'  = 180°➡ γ'  = 180° - γ = 180° - 74° = 106°

Tehát a háromszög külső szögei: 141°, 113°, 106°.

2. Feladat: Mekkorák a háromszög belső szögei, ha két külső szöge: α' = 121°, β' = 82°? Mekkora a hiányzó külső szög?

Megoldás: α és β szögek meghatározása gyerekjáték.

α + α' = 180° ➡ α = 180° - α' = 180° - 121° = 59°
β + β' = 180° ➡ β = 180° - β' = 180° - 82° = 98°

γ' meghatározásához használjuk fel az előző fejezetben tanult összefüggést, mely szerint a háromszögben egy külső szög egyenlő a nem mellette fekvő  két belső szög összegével. Így:

γ' = α  + β = 59° + 98° = 157°. Innen  γ könnyen kiszámítható: γ = 180° - γ' = 180° - 157° = 23°.

Tudjuk, hogy a háromszög belső szögeinek össze 180°, ezért az ellenőrzés könnyű: α + β + γ = 59° + 98° + 23° = 180°. Tehát jól használtuk a sháromszög külső és belső szögei közötti összefüggést.

Mit tudsz a háromszögekről? Itt tesztelheted a tudásodat:  Teszt a háromszögek szögeiről, oldalairól

Dancsó Imre
Matek- és fizikatanár