Rombusz: definíció, terület, kerület, tulajdonságok, típusok

Rombusz definíciója |  Rombusz tulajdonságai | Rombusz kerülete | Rombusz területe | Rombusz típusok | Rombusz szerkesztés | Rombuszos feladatok  

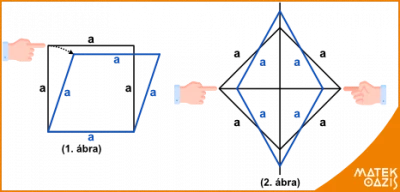
A rombusz egy speciális négyszög. Viccesen úgy is megkaphatod, hogy megpöckölsz egy négyzetet (1. ábra). Vagy úgy, ha ugyanezt a négyzetet a két sarkánál összenyomod (2. ábra).

Mi a rombusz definíciója? 

Definíció: A rombusz olyan négyszög, amelynek minden oldala egyenlő.

Minden rombusz paralelogramma és deltoid is egyben, emiatt minden tulajdonságát ötvözi ezeknek a négyszögeknek. Emlékszel, hogy mi a paralelogramma? (Olyan négyszög, amelynek szemközti oldalai párhuzamosak. Erről olvashatsz bővebben a paralelogrammáról szóló cikkünkben. A deltoid pedig olyan négyszög, melynek van a csúcsain átmenő szimmetriatengelye.

Ebben a videóban összefoglaljuk a négyszögek fajtáit és legfontosabb tulajdonságaikat. A videókkal, és egy ehhez kapcsolódó teszttel pedig alaposan begyakorolhatod ezeket.

Mik a rombusz tulajdonságai? 

Mivel minden rombusz paralelogramma is, ezért a paralelogrammák tulajdonságai természetesen mind igazak lesznek a rombuszokra is:

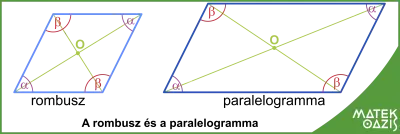
- szemközti szögei egyenlőek,

- szomszédos szögeinek összege 180°: α + β = 180°,

- középpontosan szimmetrikus,

- átlói felezik egymást.

Mik a rombuszok extra tulajdonságai, amelyek az általános paralelogrammákra nem igazak?

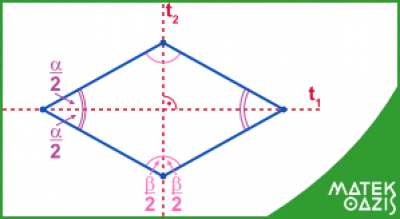
A rombusz speciális tulajdonsága, hogy tengelyesen szimmetrikus, két szimmetriatengelye (biztosan) van: az átlói. Az átlói merőlegesek egymásra, és ezek felezik a rombusz szögeit. A rombuszt az átlói négy egybevágó derékszögű háromszögre bontják.

Rombusz kerülete: hogyan számítható? 

A rombusz kerületének kiszámolásakor könnyű dolgunk van: mint minden négyszögnél, csak össze kell adnunk a négy oldal hosszát. De most ezek mind egyenlők egymással, így nagyon rövid lesz a képlet:

K = a + a + a + a = 4 ∙ a

 

Téli Kihívás​​​​​​​

November 05 - Január 12.

NYERNI AKAROK!

Rombusz területe: hogyan számítható?

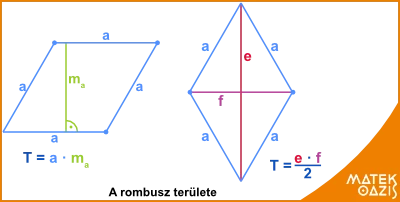
Egyrészt kiszámolhatjuk úgy, mint a paralelogramma területét: összeszorozzuk az egyik oldalának hosszát a hozzá tartozó magassággal:

T = a ∙ m_a

Másrészt deltoidként is kiszámítható a rombusz területe: ha ismerjük a két átló hosszát, akkor ezek szorzatából is megkapható a rombusz területe:

T = e ∙ f / 2

Milyen rombusz típusok vannak?

Az általános rombuszoknak az egyik szöge hegyesszög, a másik (szomszédos szöge) pedig tompaszög. Ha egy rombusz minden szöge egyenlő, akkor az már négyzet is egyben. A négyzet tehát olyan rombusz, amelynek minden szöge 90°-os, azaz minden szöge derékszög.

Hogyan lehet rombuszt szerkeszteni?

Meglepően kevés adat elég egy rombusz szerkesztéséhez, hiszen az oldalai egyenlőek. Ezért, ha adott az oldala és egy szöge, akkor abból a rombusz felét, egy háromszöget meg tudunk szerkeszteni. Utána egy tükrözés, és kész is a rombusz. (1. ábra)

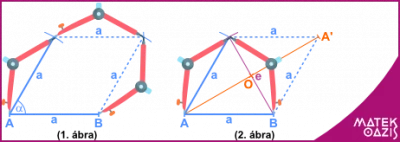
De ugyanígy elég, ha adott az oldala és egy átlója. Ezekkel az adatokkal is ugyanígy lehet elindulni a rombusz szerkesztésében. (2. ábra)

Ha a rombusz oldala és magassága adott, akkor párhuzamost kell húzni a magasságnak megfelelő távolságban, és abból lehet körzővel kimetszeni a 3. csúcsot. (3. ábra)

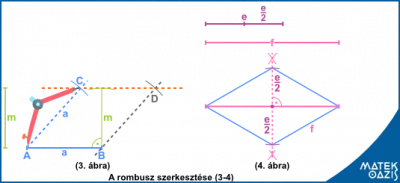
Külön eset, ha a két átlója adott. Ekkor azt a speciális tulajdonságot használjuk ki, hogy a rombusz átlói merőlegesen felezik egymást. A keletkező kis derékszögű háromszögeket meg lehet szerkeszteni, ha elfelezzük az átlókat, és ezekkel, mint befogókkal szerkesztjük meg a derékszögű háromszögeket. A rombusz ezután tükrözésekkel kiegészíthető (4. ábra).

A szerkesztésekről találsz még további részleteket ebben a 7. osztályos tankönyvben. 

Mik a rombuszhoz kapcsolódó legfontosabb feladattípusok?  

A legegyszerűbb feladattípusok a rombuszokkal kapcsolatban azok, amelyeknél csak a kerület- vagy területképletüket kell használni:

1. Feladat: Egy rombusz kerülete 20 cm. Mekkorák a rombusz oldalai?

Megoldás: K = 20 cm, a = ?

A rombusz kerület-képlete: K = 4 ∙ a

Ebbe behelyettesítjük, amit tudunk: 20 cm = 4 ∙ a,

amiből következik, hogy a = 5 cm. 

Tehát a rombusz oldalai 5 cm-esek.

2. Feladat: Egy rombusz magassága 3 cm, területe 18 cm². Mekkorák a rombusz oldalai?

Megoldás: m_a = 3 cm, T = 18 cm² , a = ?

A rombusz terület-képlete, amelyben a magassága szerepel: T = a ∙ m_a

Behelyettesítés után ebből a következőt kapjuk: 18 cm² = a ∙ 3 cm

Ebből könnyen megkapjuk, hogy a = 6 cm.

Tehát a rombusz oldalai 6 cm-esek.

3. Feladat: Egy rombusz egyik átlója 4 cm-es. Mekkora a másik átlója, ha a területe 14 cm² ?

Megoldás: e = 4 cm, T = 14 cm², f = ?

A rombusz terület-képlete, amelyben az átlói szerepelnek: T =

Ebbe, ha behelyettesítjük az adatokat, ezt kapjuk: 14 cm² = ,

amiből azt kapjuk, hogy 28 cm² = 4 cm ∙ f

Ebből következik, hogy f = 7 cm.

Tehát a rombusz másik átlója 7 cm hosszú.

Rombusszal találkozhatsz pl. összecsukható szerkezetekben

4. Feladat (8. osztálytól): Egy rombusz átlói 6 cm és 8 cm hosszúak. Mekkorák a rombusz oldalai?

Megoldás: e = 6 cm, f = 8 cm, a = ?

Ezt a feladatot mindenképpen egy vázlat rajzolásával érdemes kezdeni:

Mivel a rombusz átlói merőlegesek egymásra és felezik egymást, ezért a keletkező kis háromszögek derékszögűek, és így felírható rájuk a Pitagorasz-tétel: 3² + 4² = a²

Ebből megkapjuk, hogy a = 5. Tehát a rombusz oldala 5 cm-es.

Gyakorolj rombusszal kapcsolatos feladatokat Pitagorasz-tétel segítségével ebben a videóban.

– Tóth Viktória –

Elolvasom

Egészrész és törtrész függvény: definíció, feladatok

2024. május 27.

Mi az egészrész fogalma? Mi a törtrész fogalma? Mit kell tudni az egészrész függvényről? Mit kell tudni a törtrész függvényről?