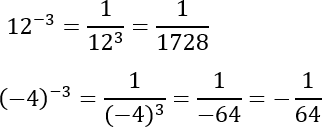A hatványozás fogalma, szabályai, azonosságai + kalkulátor

Hatványozás fogalma | Hatványozás szabályai | Hatványozás azonosságai

A hatványozás ugyanúgy egy matematikai művelet, mint az összeadás vagy a kivonás. Ha jól ismered a szabályokat, azonosságokat, akkor rengeteg időt spórolhatsz meg feladatmegoldás közben. Nézzük, mit kell tudni a hatványozásról előbb általános iskolai, majd középiskolás szinten!

Mi a hatvány, hatványozás fogalma? 

Ha sokszor össze kell adnunk egy számot önmagával, akkor az ismételt összeadást szorzással helyettesíthetjük.

Például: 4 + 4 + 4 + 4 + 4 + 4 = 6 ∙ 4 = 24 

Hasonlóan: ha sokszor össze kell szoroznunk egy számot önmagával, akkor az ismételt szorzás helyett bevezethetjük a hatványozás műveletét.

Például: 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 = 4⁶ = 4096.

4⁶ tehát egy 6 tényezőből álló szorzat, melynek minden tényezője 4. Ezt négy hatodik hatványának, vagy röviden négy a hatodikonnak hívjuk.

Elnevezések: 4 a hatványalap, azaz az ismétlődő szorzótényező, 6 pedig a hatványkitevő, ez mutatja meg, hogy hányszor ismétlődik a hatványalap a szorzatban. A 4096 megnevezése hatványérték. 

Egy szám második hatványának külön elnevezése is van, 3² hatványt nevezhetjük „3 a másodikon”-nak vagy „3 a négyzeten”-nek.
Az elnevezés onnan származik, hogy egy 3 egység oldalú négyzet területe 3²  területegység.

Egy szám harmadik hatványának is van külön elnevezése. a 4³ számot 4 köbének nevezzük.

További példák:

 6⁵ = 6 ∙ 6 ∙ 6 ∙ 6 ∙ 6 = 7776;

12³ = 12 ∙ 12 ∙ 12 = 1728

 

Téli Kihívás​​​​​​​

November 05 - Január 12.

NYERNI AKAROK!

Milyen hatványműveletek vannak? Mik a hatványozás szabályai? 

A kitevő lehet 0 és 1 is

Ekkor nyilván nem beszélhetünk 0 illetve 1 tényezős szorzatról, de megállapodás szerint bármely szám nulladik hatványa 1. FONTOS kivétel a 0, mert a „nulla a nulladikon” ( 0⁰ ) kifejezést nem értelmezzük!

Például: 5⁰ = 1;   (- 435)⁰ = 1.

Tetszőleges szám első hatványa önmaga.

Például: 3¹ = 3;    513¹ = 513;     a¹ = a.

Mit jelent, ha a hatvány alapja 0?

Ha a hatványalap 0, akkor a hatványérték minden esetben 0, hatványkitevőtől függetlenül (kivéve, ahogy már írtuk  0⁰ , mert azt nem értelmezzük).

Például: 0³ = 0;          0^74653487 = 0

Negatív alapú hatványokat hogy számolhatunk ki?

A negatív számok hatványozása ugyanúgy ismételt szorzást jelent, mint a pozitív számoknál.

Például:

(-2)⁴ = (-2) ∙ (-2) ∙ (-2) ∙ (-2) = 16;

(-3)³ = (-3) ∙ (-3) ∙ (-3) = -27;

(-4)³ = (-4) ∙ (-4) ∙ (-4) = -64

Mivel két negatív szám szorzata mindig pozitív, ezért páros darabszámú negatív szám szorzata is pozitív, és így páros kitevőjű hatványok esetén a hatványérték pozitív lesz. Amikor páratlan a kitevő, akkor a végeredmény negatív lesz.

Nézz bele ebbe az interaktív tananyagba, ha szeretnéd megismerni és begyakorolni a hatványozás alapjait!

Milyen azonosságai vannak a hatványozásnak?

Hatványok szorzását, osztását és hatvány hatványozását is egyszerűbben végezhetjük el, ha ismerjük a következő azonosságokat. Azonban fontos tudni, hogy ezek mindig azonos alapú hatványokra vonatkoznak, valamint, hogy hatványok összegére és különbségére nincsenek ilyen azonosságok!

Azonos alapú hatványok szorzása

Azonos alapú hatványokat úgy is összeszorozhatunk, hogy a közös alapot a kitevők összegére emeljük.

Például:
5³ ∙ 5⁷ = (5 ⋅ 5 ⋅ 5) ⋅ (5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5) = 5⁽³⁺⁷⁾ = 5¹⁰

4² ⋅ 4³ ⋅ 4² = (4 ⋅ 4) ⋅ (4 ⋅ 4 ⋅ 4) ⋅ ( 4 ⋅ 4) = 4^(2+3+2) = 4⁷

Emiatt a szabály miatt kell, hogy bármely szám nulladik hatványa 1 legyen, hiszen például:
2⁴ ∙ 2⁰ = 2^{4 + 0} = 2⁴

A kocka térfogatát is azonos alapú hatványok szorzásával kapjuk meg: V = a ⋅ a ⋅ a = a³

Azonos alapú hatványok osztása

Azonos alapú hatványokat úgy is oszthatunk, hogy a közös alapot a kitevők különbségére emeljük.

Például:

Hatvány hatványozása

Hatványt úgy is hatványozhatunk, hogy az alapot a hatványok szorzatára emeljük.

Például:

(5² )⁴ = 5² ⋅ 5² ⋅5² ⋅ 5² =
=(5 ∙ 5) ∙ (5 ∙ 5) ∙ (5 ∙ 5) ∙ (5 ∙ 5) = 5^(2∙4) = 5⁸

Különböző alapú, de azonos kitevőjű hatványokra is vannak azonosságok, amik egyszerűsíthetik a számolásainkat.

Azonos kitevőjű hatványok szorzása

Azonos kitevőjű hatványokat úgy is szorozhatunk, hogy az alapok szorzatát a közös kitevőre emeljük.

Például: 2³ ∙ 4³ = (2 ∙ 2 ∙ 2) ∙ (4 ∙ 4 ∙ 4) =

= 2 ∙ 4 ∙ 2 ∙ 4 ∙ 2 ∙ 4 =(2 ∙ 4) ∙ (2 ∙ 4) ∙ (2 ∙ 4) =

= (2 ∙ 4)³ = 8³

Visszafelé ez a szabály: Szorzatot úgy is hatványozhatunk, hogy a tényezők hatványait összeszorozzuk.

Például: (2 ∙ 4)³ = 2³ ∙ 4³

Azonos kitevőjű hatványok osztása

Azonos kitevőjű hatványokat úgy is oszthatunk, hogy az alapok hányadosát a közös kitevőre emeljük.

Például:

Visszafelé ez a szabály: Törtet úgy is hatványozhatunk, hogy a számlálót és a nevezőt külön hatványozzuk, majd vesszük ezek hányadosát.

Például:

Hatványozás középiskolai szinten:

Középiskolában a fentieket már készségszinten kell tudni, erre alapozva jöhetnek a további ismeretek. A hatványozást megtanuljuk negatív kitevőre, majd törtkitevőre is.

Hogyan értelmezzük egy szám negatív kitevőjű hatványát?

Negatív kitevőjű hatvány nem jelent mást, mint az ellentett, pozitív kitevőjű hatvány reciprokát

Például:

Általánosan:

Azért értelmezzük így a negatív kitevőjű hatványt, hogy minden fenti azonosság érvényes maradjon.

További példák:

Nagyon fontos, hogy pozitív számok negatív kitevőjű hatványa pozitív! Nézd meg ezt a tananyagot, ha negatív kitevőkkel is gyakorolnál.

Ha a kitevő törtszám

Az x pozitív szám a/b-edik hatványa az x alap a-adik hatványának b-edik gyöke, azaz 

Például:

Ha a kitevő negatív törtszám, akkor reciprokot kell venni ugyanúgy, mint negatív egész kitevő esetén. 

Például:

​​​​​​​

A hatványozás azonosságai negatív és törtkitevő esetén is érvényesek!

Például:

Ha más számokkal is megnéznéd ezeket az összefüggéseket, akkor kattints ide.

Elolvasom

Egészrész és törtrész függvény: definíció, feladatok

2024. május 27.

Mi az egészrész fogalma? Mi a törtrész fogalma? Mit kell tudni az egészrész függvényről? Mit kell tudni a törtrész függvényről?