Emelt szintű matematika érettségi 2022 feladatok: ezek voltak a feladatok a megoldásokkal együtt!
Dancsó Imre,
2022. augusztus 19.
Milyen feladatok voltak? | Megoldás I. (interaktív) | I. rész feladatai | II. rész feladatai
A 2022-es emelt szintű érettségi nem okozott különösebb meglepetéseket. A szokásos témakörök jelentek meg, többnyire olyan arányban, ahogy azt megszokhattuk.
A feladatsor első fele (az első négy feladat), ami mindenki számára kötelező változatos, egymástól eltérő témákat hozott. Diákbarátnak mondható feladatok voltak, de azért megjelent egy-két nehezebb részfeladat is. A második részben, ahol 5 feladat közül 4-et kell megoldani már igen sokszínűek voltak a példák. Előfordult, hogy egy feladaton belül (6.) mind a három részfeladat külön témakörrel foglalkozott. A feladatsor nem volt könnyű, sokat kellett számolni benne és profin tudni az összefüggéseket, de nagy varázslatot nem igényeltek a példák. de úgy gondoljuk mindenki ki tudta választani azt az egy példát, ami számára barátságtalan.
Emelt szintű matematika érettségi 2022: milyen feladatok voltak?
Itt egy gyors összefoglaló, hogy melyik témakörből mennyi pontot lehetett szerezni az érettségin. Meglepetésnek számít, hogy az előző évi májusi feladatsorhoz képest mekkora az eltérés.
1. helyezett: Egyenletek és algebra 25 pont
2. helyezett: Függvények és analízis 15 pont
3. helyezett: Valószínűségszámítás 15 pont
4. helyezett: Sorozatok és Síkgeometria 13-13 pont
5. helyezett: Kombinatorika és Koordinátageometria 11-11 pont
6. helyezett: Térgeometria 8 pont
7. helyezett: Gráfok 7 pont
8. helyezett: Százalékszámítás és Statisztika 5-5 pont
Nézzük részletesen a feladatokat – megoldásokkal együtt!
Itt megtalálod a 2022-es emelt szintű matematika érettségi 1-3. feladatait interaktív megoldásokkal, amikből nagyon sokat tanulhatsz:
Részlet a 2022.-es melet szintű érettségi I. rész interktív videóból
Hasonló interaktív videókon átnézhetsz minden matek érettségi témakört, és begyakorolhatod az érettségi feladatok megoldását.
Többet akarok tudni az érettségi felkészítésről
Ezek voltak a feladatok (I. rész):
1. Oldja meg a valós számok halmazán az alábbi egyenleteket!
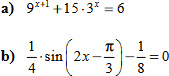
2.
a) Egy számtani sorozat első tagja 5, differenciája 3, az első n tag összege pedig 4900. Határozza meg n értékét! (5 pont)
b) Egy mértani sorozat első és második tagjának összege 6, harmadik és negyedik tagjának összege pedig 96. Adja meg a sorozat első tagját és hányadosát! (8 pont)
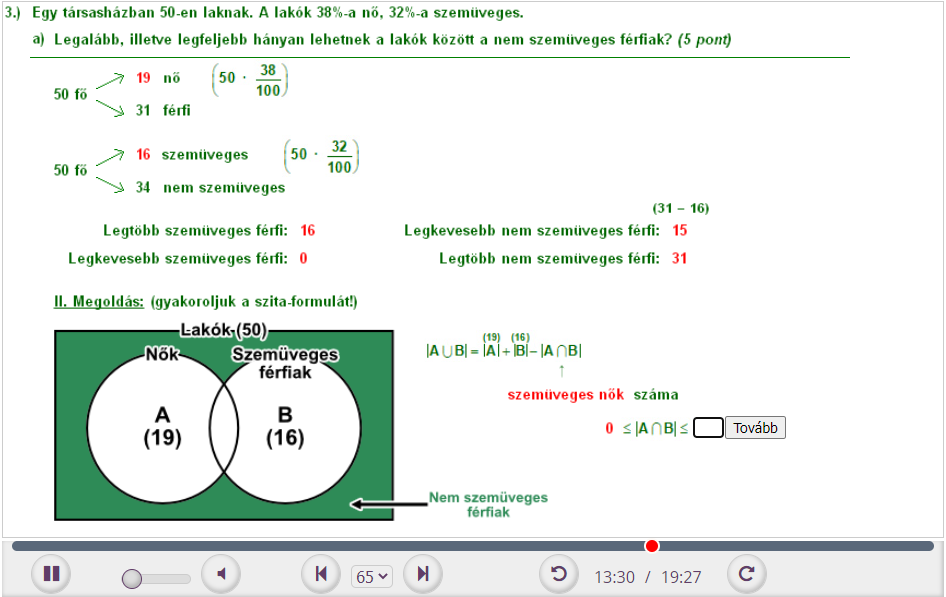
3.) Egy társasházban 50-en laknak. A lakók 38%-a nő, 32%-a szemüveges.
a) Legalább, illetve legfeljebb hányan lehetnek a lakók között a nem szemüveges férfiak? (5 pont)
A társasház kertje egy 15 méter hosszú, 10 méter széles téglalap alakú földterület, amely az egyik átlója mentén ketté van osztva: az egyik fele füvesítve van,
a másik felén virágágyás található. A füvesített rész derékszögű csúcsában van egy öntöző, amely egy 10 méter sugarú negyedkör alakú területet locsol a kertben.
b) Mekkora az a füvesített terület, amelyet nem ér el az öntöző? (8 pont)
4. Egy biliárdgolyó készletben található 9 golyó tömegére a következő mérési eredményeket kapták (grammban): 163, 163, 163, 163, 163, 164, 165, 166, 166.
Egy ilyen készletet akkor hitelesítenek a minőségellenőrzésen, ha az alábbi feltételek mindegyikének megfelel:
- minden golyó tömege legalább 160 gramm és legfeljebb 170 gramm;
- a golyók tömegének terjedelme legfeljebb 3 gramm;
- a golyók tömegének szórása legfeljebb 1 gramm.
a) Hitelesíthető-e ez a készlet? (5 pont)
Egy dobozban 3 piros és 7 kék golyó található.
b) Kihúzunk a dobozból egymás után két golyót úgy, hogy az elsőként kihúzott golyót a húzás után nem tesszük vissza. Határozza meg annak a valószínűségét,
hogy a kihúzott két golyó között lesz piros! (4 pont)
c) Kihúzunk a 10 golyó közül egymás után három golyót úgy, hogy a kihúzott golyót a következő húzás előtt mindig visszatesszük. Legyen az A esemény az,
hogy a kihúzott három golyó közül pontosan kettő piros, a B esemény pedig az, hogy a kihúzott golyók között van piros.
Határozza meg a P(A | B) valószínűséget! (5 pont)
A 2022. emelt szintű érettségi feladatok II. része:
Többet akarok tudni az érettségi felkészítésről
5. Lali, Pali és Vali egy palacsintázóban ebédelnek. Lali 3 mogyorókrémes, 1 túrós és 2 fahéjas palacsintáért 1500 Ft-ot, Pali 4 mogyorókrémes, 2 túrós és 1 fahéjas palacsintáért
1740 Ft-ot, Vali pedig 1 mogyorókrémes, 2 túrós és 2 fahéjas palacsintáért 1170 Ft-ot fizetett.
a) Mennyibe kerül 1-1 darab a különböző fajta palacsintákból? (8 pont)
Lali vesz még egy lekváros palacsintát 210 Ft-ért. Lali zsebében 100, 50, 20, 10 és 5 Ft-os érmék vannak, mindegyikből több is. Ezek közül 6 érmét választ ki.
b) Igazolja, hogy 6 érmével három különböző módon fizethető ki 210 Ft! (Két fizetést különbözőnek tekintünk, ha legalább az egyik címletű érméből eltérő számút
használunk fel a két fizetés során.) (5 pont)
c) Hányféle sorrendben vehet elő Lali 6 olyan érmét a zsebéből, amelyek összege 210 Ft, ha egyesével húzza elő őket? (Az azonos címletű érméket nem
különböztetjük meg egymástól.) (3 pont)
6. Egy egyenlőszárú háromszög csúcsai a derékszögű koordináta-rendszerben A(0 ; 0), B(82 ; 0) és C(41 ; 71). Géza szerint ez a háromszög szabályos.
a) Határozza meg a háromszög szögeit fokban, három tizedesjegyre kerekítve! (5 pont)
b) Határozza meg a háromszög AC és AB oldalainak arányát négy tizedesjegyre kerekítve! (3 pont)
Egy csonkakúp alapkörének sugara 14 cm, fedőkörének sugara 8 cm, alkotója 10 cm hosszú. Géza szeretné gyorsan megbecsülni a csonkakúp térfogatát,
ezért azt egy henger térfogatával közelíti. A közelítő henger alapkörének sugara megegyezik a csonkakúp alap- és fedőköre sugarának számtani közepével,
magassága pedig egyenlő a csonkakúp magasságával.
c) Határozza meg Géza közelítésének relatív hibáját! (Relatív hibának nevezzük a közelítő értéknek a pontos értéktől mért százalékos eltérését.) (8 pont)
7. Flóra kétfajta lisztből süt kenyeret. A kenyérhez a recept alapján 5 : 4 arányban kell búzaliszt és rozsliszt. Eredetileg 450 gramm búzalisztet és 400 gramm rozslisztet
kevert össze, de további, összesen 500 gramm liszt hozzáadásával sikerült elérnie a recept által előírt arányt.
a) A hozzáadott 500 gramm lisztből hány gramm volt a búzaliszt? (3 pont)
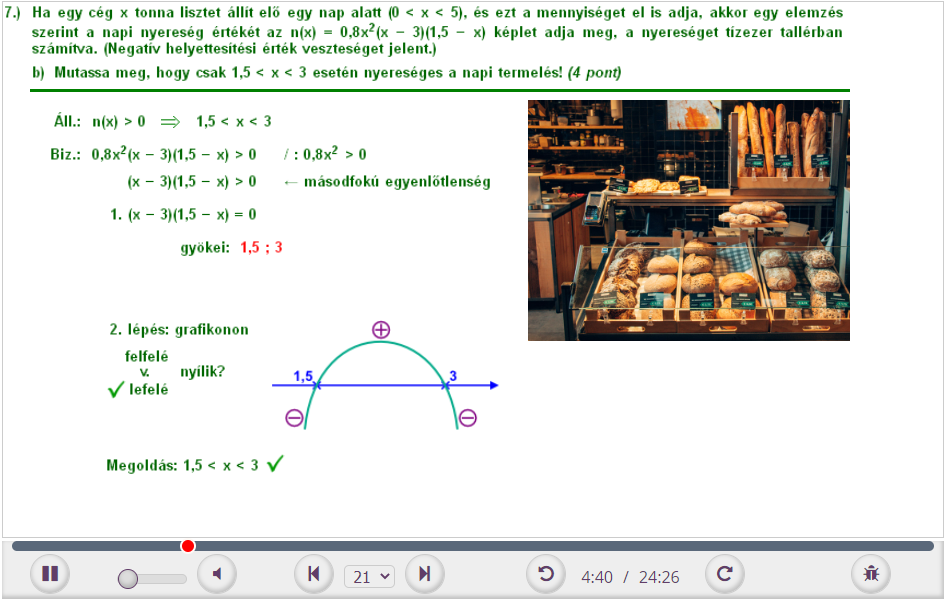
Ha egy cég x tonna lisztet állít elő egy nap alatt (0 < x < 5), és ezt a mennyiséget el is adja, akkor egy elemzés szerint a napi nyereség értékét az
n(x) = 0,8x2(x − 3)(1,5 − x) képlet adja meg, a nyereségét képlet adja meg, a nyereséget tízezer tallérban számítva. (Negatív helyettesítési érték
veszteséget jelent.)
b) Mutassa meg, hogy csak 1,5 < x < 3 esetén nyereséges a napi termelés! (4 pont)
c) Hány tallér az elérhető legnagyobb napi nyereség, és ezt hány tonna liszt (előállítása és eladása) esetén érik el? (9 pont)
8. Egy baráti összejövetelen 7 fiú és 5 lány vett részt, találkozáskor mindenki üdvözölte a többieket. A fiúk kézfogással köszöntek egymásnak, két lány, illetve egy fiú és
egy lány pedig öleléssel köszöntötte egymást.
a) Hány olyan találkozás volt, ahol öleléssel köszöntötték egymást? (3 pont)
Egy hatfős baráti társaság tagjai András, Bori, Csaba, Dóra, Ervin és Fanni bajnokságon döntik el, hogy ki a legjobb pingpongos közülük. Mindenki mindenki ellen
egy mérkőzést játszik. Amikor 9 mérkőzést már lejátszottak, akkor kiderült, hogy mindegyikük páratlan számú mérkőzésen van túl. András az eddigi egyetlen
meccsét Bori ellen játszotta, Csaba még nem játszott Ervin ellen.
b) Játszott-e már Dóra Fanni ellen? (7 pont)
András, Bori, Csaba és Dóra egy szabályos dobókockával dobnak egyet-egyet, és az nyer, aki a legnagyobb olyan számot dobta, amit a többiek nem dobtak
(például 6, 6, 4, 1 dobások esetén a 4-est dobó játékos nyer). Ha nincs ilyen szám, akkor nem nyer senki. Bori 5-öst dobott, a többiek ezután fognak dobni.
c) Mennyi a valószínűsége annak, hogy Bori nyer? (6 pont)
9. Adott az x2 + 2y = 16 egyenletű parabola é az x2 + (y − 3)2 = 9 egyenletű kör.
a) Határozza meg a parabola fókuszpontjának és a kör középpontjának a koordinátáit! (4 pont)
b) Igazolja, hogy a Q(2√2;4) pont a parabolának és a körnek is pontja, és a kör Q-ban húzott érintője érinti a parabolát is! (7 pont)
c) Határozza meg a parabola és az x tengely által közrezárt korlátos síkidom területét! (5 pont)
A feladatokat és a megoldókulcsot innen letöltheted:
(forrás: OM)
Ha sok hiányosságod van még, az intenzív tréninggel bepótolhatod, és egy klassz érettségit írhatsz!
Hihetetlenül gyorsan tudsz fejlődni matekból az egyedi módszereknek és a jól felépített tananyagnak köszönhetően.
Többet akarok tudni az érettségi felkészítésről
Matek- és fizikatanár
Mi a szögfelező egyenes definíciója? Milyen tulajdonságai vannak a szögfelező egyenesnek? Mit mond ki a szögfelezők metszéspontjára vonatkozó tétel? Hogy kell bizonyítani a szögfelezők metszéspontjára vonatkozó tételt?
Belső szögfelezők metszéspontjára vonatkozó tétel bizonyítása
2024. február 23.