Trapéz
Az olyan négyszögeket hívjuk trapéznak, amiknek van párhuzamos oldalpárjuk.
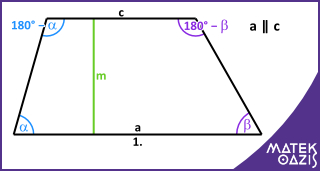
Az ábrán az "a" és "c" oldalak a párhuzamos oldalpárok, ezeket alapnak hívjuk. A nem párhuzamos két oldalt hívjuk szárnak. A trapéz egy száron fekvő szögeinek az össze 180°.
3 fajta trapézt szoktunk megkülönböztetni:
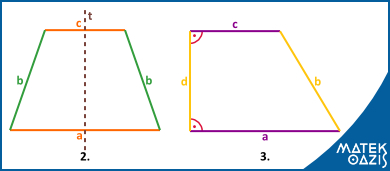
Általános trapéz (1)
Egyenlő szárú trapéz (2): Az alapon fekvő szögei ugyanakkorák. Másik elnevezései: húrtrapéz, szimmetrikus trapéz. (A t szimmetriatengely felezi az alapokat)
Derékszögű trapéz (3): Olyan trapéz, aminek van két derékszöge
A trapéz kerülete: 
A trapéz terülte: 
, ahol m a trapéz magassága.
Példák trapézzal kapcsolatos számításokra:
1. feladat: Egy derékszögű trapéz egyik szöge 39°-os. Mekkorák a trapéz szögei?
Megoldás: Egy derékszögű trapéznak két derékszöge van, azaz két 90°-os szöge. Az egy száron fekvő szögek összege 180°, ezért a hiányzó szög nagysága: 180° - 39° = 141°.
2. feladat: Egy trapéz egyik alapja 10 cm hosszú, a másik pedig 30 cm. A trapéz magassága 25 cm. Mennyi a trapéz területe?
Megoldás: 
Mindent cm-ekben számolva:
A kövekező Matek Oázis videókkal tanulhatsz a trapézról
Felvételi feladatsor: 2008 M2 1-5. feladat
Oldjuk meg együtt a 2008-as felvételi feladatsor 2. feladatlapjának első feladatait! Algebrai számításokat végzünk. Keresd meg az összes lehetőséget: hány trapéz jön létre a háromszögekben? Mértékegység átváltásokra kerül sor. Adatokat olvasunk le grafikonról, szöveges feladatokat végzünk.
3. feladatsor
Újabb feladatsort találsz ezen a videón nyolc feladattal (megoldások nélkül) a 9. osztályos tananyagból. A feladatok önálló megoldásával tovább tesztelheted matematikai tudásod. Algebrai átalakításokat kell végezned. Mekkora a háromszög területe, az átfogója és a köré írható kör sugara? Törtes egyenlet, függvényábrázolás, Egyenlőtlenség grafikus megoldása, szöveges feladat, húrtrapéz (területe, átlói, oldalai), átlag, medián, kördiagram készítése kerül elő a feladatok között.
3. feladatsor megoldásai
Az előző videó feladatsorának megoldásait mutatjuk be ezen a videón magyarázatokkal. Igaz vagy hamis? Algebrai átalakításokat végzünk. Mekkora a háromszög területe, az átfogója és a köré írható kör sugara? Törtes egyenlet kiszámítására, függvényábrázolásra, egyenlőtlenség grafikus megoldására, szöveges feladat megoldására, húrtrapézzal kapcsolatos feladat megoldására (területe, átlói, oldalai), átlag, medián kiszámítására, kördiagram készítésére kerül sor.
Felvételi feladatsor: 2008 M1 1-6. feladat
A 2008 májusi felvételi feladatsor első részét nézzük át együtt. Rövid műveleteket végzünk, szöveges feladatokat oldunk meg, gyakoroljuk a műveleteket mértékegységekkel, az átváltásokat, grafikont értelmezünk, egyenlettel megoldható szöveges feladat és geometria (szimmetrikus trapéz oldalai, szögei) is van ebben a feladatsorban. (8.-os felvételi feladatsor, 6.-osoknak)
Felvételi feladatsor: 2008 M2 1-5. feladat
Oldjuk meg együtt a 2008-as felvételi feladatsor 2. feladatlapjának első feladatait! Algebrai számításokat végzünk. Keresd meg az összes lehetőséget: hány trapéz jön létre a háromszögekben? Mértékegység átváltásokra kerül sor. Adatokat olvasunk le grafikonról, szöveges feladatokat végzünk. (8.-os felvételi feladatsor, 6.-osoknak)
Felvételi feladatsor: 2004 M2 7-10. feladatok megoldásai
A 2004. évi felvételi feladatsor megoldásait találod ezen a videón. Grafikon értelmezése; Dobókockás feladat; Egyenlettel megoldható szöveges feladat; Geometriai szöveges feladat (derékszögű trapéz szögei, oldalai). (8.-os felvételi feladatsor, 6.-osoknak)
22. Területszámítás és integrálás ...
22. Tétel: Területszámítás elemi úton és az integrálszámítás felhasználásával. A tétel kifejtésében a területszámításról fogunk beszélni. Először elemi úton vizsgáljuk meg a témát, síkgeomatriai alakzatok területét részletezzük, majd áttérünk az integrálszámítás felhasználására. A tételt hallani fogod, és látni azt, amit közben érdemes a táblára írnod. Hogyan lehet definiálni egy alakzat területét? A területet úgy értelmezzük, mint egy függvényt, ahol minden síkidomhoz hozzárendelünk egy pozitív számot 3 tulajdonsággal. Ezek a következők: Az egységnégyzet területe 1. Az egybevágó sokszögek területe egyenlő. A 3. tulajdonság pedig úgy szól, hogy ha egy sokszöget feldarabolunk részsokszögekre, akkor a részek területének összege a sokszög területével egyenlő. Hogyan számoljuk ki különböző sokszögek területét? A sokszögek esetén a terület nagyságának meghatározása az egységnyi területtel való összevetés alapján történik. Ezt a szerepet tölti be az egységnégyzet. Nézzük át néhány speciális sokszög területének kiszámítási módját! A téglalap területe két szomszédos oldalának szorzatával egyenlő. A paralelogramma területe az egyik alap és a hozzátartozó magasság szorzata. Részletezzük a háromszög területének képletét, a trapéz területének kiszámítását. Mivel minden sokszög véges számú háromszögre darabolható, ezért a sokszög területe egyenlő a háromszögek területösszegével. A háromszög területének kiszámítására sok képlet van, ezek közül felírtam a leggyakrabban használtakat. Ezekben a képletekben s a félkerület, az r a beírt kör sugara, R pedig a háromszög körülírt körének a sugara. Azt a tételt bizonyítjuk, hogy átalános négyszög területét úgy számíthatjuk ki, hogy az átlók hosszát megszorozzuk a közre zárt szögük szinuszával, és ezt a szorzatot osztjuk kettővel. A bizonyítást a videón részletezzük. Szabályos sokszögek területét úgy kapjuk meg, hogy a középpontjukat összekötjük a csúcsokkal és így n db egyenlő szárú háromszöget kapunk, ezek területe már a középponti szög és a sugár ismeretében kiszámolható. Kör területének kiszámítása. Tétel: Az r sugarú kör területe r2pi-vel egyenlő. Mi a kapcsolat a területszámítás és az integrálszámítás között? A határozott integrállal függvénygörbe vonalával határolt síkidomok területét tudjuk meghatározni. A határozott integrál definíciójához szükségünk van még az intervallum felosztásának a definíciójára. Utána vesszük ennek a felosztásnak egy intervallumát, például az [xi-1;xi] zárt intervallumot. Kis mi legyen az f függvénynek ebben az intervallumban felvett értékeinek alsó határa, nagy Mi pedig a felső határa. Korlátos függvényeknél bizonyítható, hogy ezek az értékek léteznek. Az [xi-1;xi] intervallum fölé téglalapokat szerkesztünk, kettő darabot, kis mi, illetve nagy Mi magassággal. Ha ezt a felosztás összes intervallumában elvégezzük, megkapjuk a vizsgált tartomány egy körülírt és egy beírt sokszögét. Ezeknek a sokszögeknek vizsgáljuk meg a területét. A beírt sokszög területét alsó közelítő összegnek hívjuk, a körülírt sokszög területét pedig felső közelítő összegnek hívjuk. A felosztást finomíthatjuk. Így végtelen sok alsó és felső összeg keletkezik, amelyekről elmondható, hogy semelyik alsó összeg nem lehet nagyobb semelyik felső összegnél. Most már tudjuk definiálni a határozott integrált: Az [a; b] intervallumon korlátos, f függvény integrálható, ha bármely, minden határon túl finomodó felosztássorozatához tartozó alsó és felső összegei sorozatának közös határértéke van. Ezt a közös határértéket nevezzük az f függvény [a; b] intervallumon vett határozott integráljának. Két függvény által közrezárt síkidom területe is kiszámolható a határozott integrállal. Ha f(x)>g(x), akkor az f és g függvények görbéi által közrezárt síkidom területe az f – g függvény integrálásával számolható. A tételt matematika-történeti vonatkozások és gyakorlati alkalmazáshoz kapcsolódó példák zárják. A tétel végén pedig segítünk megtanulni is a tételt, gyakorolhatsz a saját tempódban.
Négyszögek szerkesztése - négyzet, téglalap, rombusz
Speciális négyszögek szerkesztése. Ebben a videóban négyszögek szerkesztését tanuljuk meg. Körzővel és vonalzóval szerkesztjük meg a négyzetet, téglalapot, rombuszt. Az alapos begyakorláshoz ceruzára, papírra, vonalzóra és körzőre is szükséged lesz.
Négyszögek szerkesztése - trapéz, deltoid
Speciális négyszögek szerkesztése - folytatás. Folytatjuk a négyszögek szerkesztését. Körzővel és vonalzóval szerkesztünk rombuszt, szimmetrikus trapézt (húrtrapéz), deltoidot. Az alapos begyakorláshoz ceruzára, papírra, vonalzóra és körzőre is szükséged lesz.
