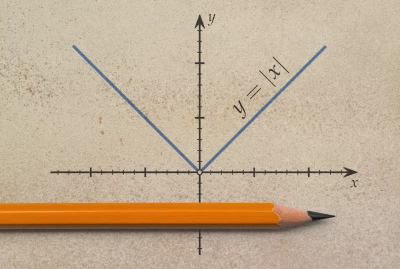Függvény
Minden függvényhez kell két halmaz: egy alaphalmaz és egy képhalmaz. Ha az alaphalmaz minden eleméhez hozzárendeljük a képhalmaz valamelyik elemét, és ez a hozzárendelés egyértelmű, akkor ezt a hozzárendelést függvénynek nevezzük.
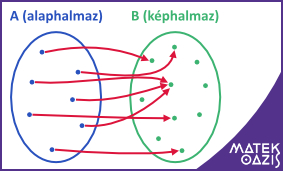
Az alaphalmaz neve értelmezési tartomány. Az elemek képét függvényértéknek nevezzük.
A függvényértékek halmazának a neve értékkészlet.
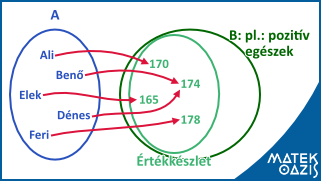
Matekórán leggyakrabban szám → szám függvényekkel foglalkozunk. Ez azt jelenti, hogy az alaphalmaz és a képhalmaz is számhalmaz.
Az ilyen függvényeket tudjuk grafikon segítségével ábrázolni derékszögű koordinátarendszerben. Ezt a grafikont úgy kapjuk meg, ha ábrázoljuk azokat a pontokat, amelyeknek az első koordinátája az értelmezési tartomány valamelyik eleme, a második koordinátája pedig az ehhez rendelt függvényérték. A függvények leggyakrabban használt jelölése: f (x).
Példák függvényábrázolásra
1. feladat: Legyen f (x) függvény olyan, hogy minden hatnál kisebb pozitív egész számhoz hozzárendeli a nála 1-gyel kisebb számot. Készítsünk érték táblázatot és ábrázoljuk ezeket a pontokat!
Megoldás:
| x | 1 | 2 | 3 | 4 | 5 |
| y | 0 | 1 | 2 | 3 | 4 |
A hatnál kisebb pozitív egész számok az 1 ; 2 ; 3 ; 4 ; 5. Ezekhez a számokhoz rendeljük hozzá a náluk 1-gyel kisebb számokat. Tehát az x = 1-hez az y = 0 értéket. Az x = 2-höz az y = 1-et és így tovább.
Az első pontot úgy tudjuk ábrázolni, hogy a derékszögű koordinátarendszer vízszintes x tengelyén megkeressük az x = 1 helyet. Ehhez a helyhez az y = 0 érték tartozik. Vagyis az első ábrázolt pont koordinátái (1 ; 0). A többi pont ábrázolása hasonlóan történik.
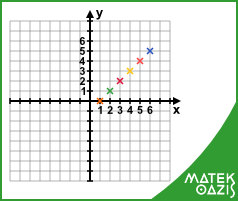
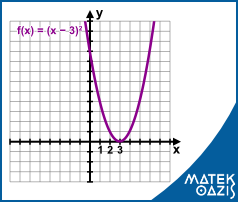
2. feladat: Ábrázoljuk az f (x) = (x - 3)2 függvényt! (8. osztálytól)
A sima x2 függvényhez képest ezt úgy tudjuk ábrázolni, hogy az x tengely mentén víszintes irányban eltoljuk jobbra a grafikont 3 egységgel. (Hiszen pl. x=3 helyen a függvényérték: (3-3)2 = 0; x=4 helyen (4-3)2 = 1; (2-3)2 = 1; stb..)
A következő Matek Oázis videókkal tanulhatsz a függvényekről
Másodfokú függvények
TESZT! Feladatok: Melyik függvény grafikonját látod? Add meg a hozzárendelési szabályt! Ábrázold a függvényt! Merre kell eltolni a parabolát? Merre fog állni a parabola? Hol metszi a grafikon az x tengelyt? Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Abszolútérték függvény
TESZT! Gyakorlófeladatok: Készítsd el a függvény grafikonját! Merre kell eltolni az f(x) függvény grafikonját? Hol metszi a grafikon az y tengelyt? Írd fel az f(x) függvény hozzárendelési szabályát! Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.
Függvény-transzformációk 1. rész
Ezen a videón nagyon látványosan mutatjuk be a legalapvetőbb függvénytranszformációkat. Azokat a függvénytranszformációkat gyakorolhatod itt be a másodfokú függvények példáján, melyek a függvények x-tengellyel illetve y-tengellyel párhuzamos eltolását eredményezik. Merre toljuk el a függvény grafikonját, ha a függvény értékéhez adunk hozzá (értékéből vonunk ki) egy számot? Merre toljuk el a függvény grafikonját, ha az x értékéhez adunk hozzá (értékéből vonunk ki) egy számot? Ezekre a kérdésekre kaphatsz kimerítő választ.
Függvény-transzformációk 2. rész
Ez a videó függvénytranszformációk közül a függvények nyújtásával foglalkozik. Ha egy számmal szorzunk egy függvényt, akkor az y tengely irányában vagy nyújtani kell, vagy épp ellenkezőleg, "össze kell nyomni". És az sem mindegy, hogy pozitív, vagy negatív számmal szorzunk. Ezzel a videóval az ilyen típusú transzformációkat alaposan begyakorolhatod.
Függvény-transzformációk 3. rész
Ebben a videóban gyakorolhatod mindazt, amit a függvénytranszformációkról megtanultál. A másodfokú függvényekkel kell különböző transzformációkat végezni, az ellenőrzés pedig nagyon egyszerű: csak ki kell választanod, hogy milyen irányban kell eltolni a függvényt, vagy hogy nyújtani kell-e, és hogy merrefelé nyílik a parabola. Ha ezeket a függvénytranszformációs videókat végignézed, már nem fog gondot okozni, ha ilyen feladatot kapsz.
Fontosabb függvények
Ezen a matematikai oktatóvideón a fontosabb függvénytípusokat vesszük sorra: lineáris függvények, másodfokú függvények, hatványfüggvények, abszolútérték-függvény, négyzetgyökfüggvény, és a törtfüggvények. Hogyan kell ábrázolni ezeket a függvényeket? Mi jellemzi őket szélsőérték, monotonitás, zérushely szempontjából, páros vagy páratlan-e a függvény.
Függvények határértéke
Függvény jobb és bal oldali határértékéről tanulunk. Példákat oldunk meg jobb és bal oldali határértékre. Megnézzük, hogyan lehet a végtelen határérték. További függvények határértékét vizsgáljuk. Gyakorló feladatokat oldunk meg a függvények határérték számításával kapcsolatosan.
Fogalmak, néhány függvény deriváltja
A differenciálszámítással az analízis egyik fontos mérföldkövéhez érkeztünk. Megtanuljuk mi a differenciahányados és differenciálhányados fogalma, mi a deriváltfüggvény. Meghatározzuk néhány függvény deriváltját: pl. sin x, cos x, ln x ... Példákkal, feladatokkal gyakorlunk.
Hegyesszögek szögfüggvényei
JÁTÉK! Telepítsd be a tengeri akváriumot! Derékszögű háromszögekben keressük az alfa vagy a béta szög szögfüggvényeit. El kell döntened, hogy a felírt tört a megadott szög szinuszával, koszinuszával, vagy épp tangensével-kotangensével egyezik meg. Látni fogod utána a magyarázatot is, így a végére már magabiztosan fogod tudni használni a szögfüggvényeket.
Függvények érettségi feladatokban I.
Függvényes érettségi feladatok I. A mostani matekvideóban az elmúlt évek májusi érettségi feladatai közül oldunk meg néhányat, amelyekben felhasználjuk azt a tudást, amit elsajátítottunk a függvényekkel kapcsolatban. Találkozunk egészen könnyű, ábrázolós feladatokkal és igazán nehéz analízis példákkal is.
Függvények érettségi feladatokban II.
Függvényes érettségi feladatok II. Mivel az emeltszintű érettségin minden évben van függvényes feladat, ezért megnézünk még néhány szép feladatot májusi feladatsorokból. Sok típuspélda előfordul ebben a videóban, amik begyakorlásával kellő rutint szerezhetünk a gyors és pontos feladatmegoldáshoz.
Függvények, függvényjellemzés - folytatás
Meghatározzuk a zérushelyet, a szélsőértéket, a maximum- és minimum helyet (értéket). Megrajzoljuk a függvény grafikonját. A függvények tulajdonságaival foglalkozunk, ez a függvényjellemzés. Mi az értékkészlete, az értelmezési tartománya a függvénynek, csökkenő vagy növekvő a függvény?
Szögfüggvények derékszögű háromszögekben - fogalmak
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón!
Elsőfokú függvények - alapok
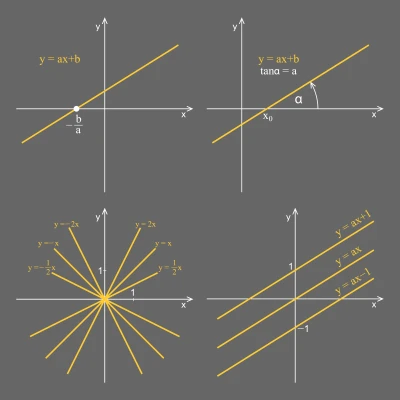
Bevezetünk a függvények világába. Lineáris függvényeket ábrázolunk koordináta-rendszerben: grafikonjuk egyenes f(x) = ax + b , ahol a a meredekség, és b-ben metszi az y-tengelyt; b=0 esetén az origó a függvénypontjuk. Megmutatjuk a lépkedéses módszert és az értéktáblázatot. Példákkal gyakorlunk.
Négyzetgyökfüggvény, törtfüggvény
Ez a videó további függvényekkel kapcsolatos ismeretek gyakorlására szolgál. Négyzetgyök-függvény, törtfüggvény. A függvények jellemzését gyakorolhatod ezekkel a feladatokkal. Értelmezési tartomány és értékkészlet, zérushely, növekedés-fogyás (csökkenés), valamint a szélsőértékek (minimum és maximum), sőt: páros és páratlan függvény. Mindegyikkel tisztában vagy, mit jelent?
Egészrész-, törtrész- és előjel-függvény
Az egészrész és törtrész-függvény ábrázolását, a függvények jellemzését gyakorolhatod ezekkel a feladatokkal. Értelmezési tartomány és értékkészlet, zérushely, növekedés-fogyás (csökkenés), valamint a szélsőértékek (minimum és maximum), sőt: páros és páratlan függvény. Mindegyikkel tisztában vagy, mit jelent?
Szögfüggvények derékszögű háromszögekben
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón, és gyakoroljunk közösen!
