Tangens szögfüggvény a derékszögű háromszögben
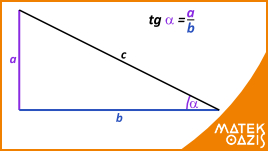
Legyen α egy tetszőleges derékszögű háromszög egyik hegyesszöge. Ekkor a háromszögben az α szöggel szemben elhelyezkedő befogó és az α szög melletti befogó hosszának a hányadosa állandó (független az oldalak nagyságától, és csak α-tól függ). Ezt nevezzük tanges α-nak, és tg α - val jelöljük .
Példa a tangens gyakorlásához
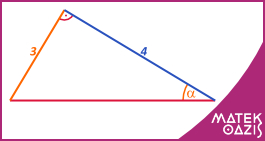
Feladat: Egy derékszögű háromszög két befogója 3 illetve 4 egység hosszú. α legyen a 3 egységnyi befogóval szemközti szög! Számítsuk ki α tangensét!
Készítsünk ábrát! A két befogó mindig merőleges egymásra, és a derékszögű háromszög két rövidebb oldala. Pl:
A következő Matek Oázis videókkal tanulhatsz a tangens szögfüggvényről
Trigonometrikus egyenlőtlenségek
Az egyenletek után a trigonometrikus egyenlőtlenségek megoldásával is foglalkozunk. Tisztázzuk a tudnivalókat a nevezetes szögekről, meghatározzuk a tartományt, a periódust, amiben számolunk. Szinusz, koszinusz, tangens, kotangens szögfüggvényekkel is dolgozunk. Feladatokat oldunk meg a trigonometrikus egyenlőtlenségek megoldásának gyakorlására.
Hegyesszögek szögfüggvényei
JÁTÉK! Telepítsd be a tengeri akváriumot! Derékszögű háromszögekben keressük az alfa vagy a béta szög szögfüggvényeit. El kell döntened, hogy a felírt tört a megadott szög szinuszával, koszinuszával, vagy épp tangensével-kotangensével egyezik meg. Látni fogod utána a magyarázatot is, így a végére már magabiztosan fogod tudni használni a szögfüggvényeket.
Szögfüggvények derékszögű háromszögekben - fogalmak
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón!
Szögfüggvények derékszögű háromszögekben
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón, és gyakoroljunk közösen!
