Paralelogramma
Azokat a négyszögeket hívjuk paralelogrammának, amelyekben a szemközti oldalak párhuzamosak.
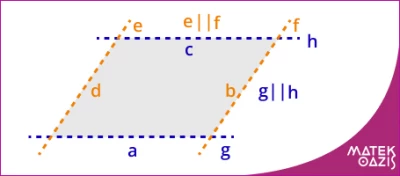
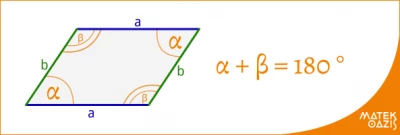
A paralelogrammának két-két szemközti oldala egyenlő hosszú.
A paralelogramma szemközti szögei egyenlő nagyságúak. Bármely két szomszédos szögének összege 180°.
A paralelogramma átlói felezik egymást.
A paralelogramma középpontosan szimmetrikus négyszög (a szimmetria középpont az átlók metszéspontja).
Példák paralelogrammával
1. Feladat: Döntsük el a következő állításokról, hogy igaz vagy hamis!
a) A paralelogramma átlói egyenlő hosszúak.
b) Minden négyzet paralelogramma.
Megoldás:
a) Az állítás hamis. A legtöbb paralelogrammának különböző hosszúak az átlói, csak a téglalapok olyan paralelogrammák, amiknek az átlói ugyanolyan hosszúak (a téglalap speciális paralelogramma, hiszen szemközti oldalai párhuzamosak).
b) Az állítás igaz, hiszen minden négyzetnek párhuzamosak a szemközti oldalai.
2. Feladat: Egy paralelogramma egyik szöge: ɑ = 53°. Mekkora a másik három szöge?
Megoldás: Mivel az egymás melletti szögek összege 180°, ezért az 53°-os szög mellett 127°-os szög van. A paralelogrammában a szemközti szögek egyenlők, ezért a másik hiányzó két szög közül az egyik 53°-os, a másik pedig 127°-os.
A következő Matek Oázis videókkal tanulhatsz a paralelogrammáról
Vektorok - Vektorműveletek
A vektorok irányított szakaszok. Először azokat a vektorokkal kapcsolatos ismereteket nézzük át, amelyekkel valószínűleg már találkoztál. Vektorműveleteket végzünk, vektorokat adunk össze és vonunk ki egymásból, vektort számmal szorzunk összefűzés, paralelogramma módszerével. Elmondjuk, mikor melyik módszert érdemes vagy kell alkalmazni. Megismerkedünk a helyvektor és a háromszög súlypontjába mutató helyvektor fogalmával. Vektoros feladatokat oldunk meg együtt.
Vektorok (ismétlés)
A vektorok irányított szakaszok. Először azokat a vektorokkal kapcsolatos ismereteket nézzük át, amelyekkel valószínűleg már találkoztál. Vektorműveleteket végzünk, vektorokat adunk össze és vonunk ki egymásból, vektort számmal szorzunk összefűzés, paralelogramma módszerével. Elmondjuk, mikor melyik módszert érdemes vagy kell alkalmazni. Megismerkedünk a helyvektor és a háromszög súlypontjába mutató helyvektor fogalmával. Vektoros feladatokat oldunk meg együtt.
2. feladatsor (11. osztály)
Újabb hat feladat (megoldások nélkül) a 11. osztályos tananyagból. Ezek megoldásával kiderítheted, vannak-e hiányosságaid, illetve még jobban rögzítheted mindazt, amit tudsz. Exponenciális függvény ábrázolása, exponenciális-, logaritmikus-, trigonometrikus egyenletek, paralelogramma oldalainak kiszámítása vár, valamint egy koordinátageometriai feladat: Kör és az érintő egyenletének felírása.
Vektorok - összefoglalás
Ez a videó a vektorokkal kapcsolatos ismereteket foglalja össze. Ezekkel az irányított szakaszokkal is lehet különböző műveleteket végezni (de persze nem úgy, mint a számokkal). Hogyan lehet elvégezni a vektorok összeadását (paralelogramma módszerrel ill. összefűzéssel), vektorok kivonását, hogyan lehet őket számmal szorozni, illetve mit jelent vektorok skaláris szorzata, ezeket nézzük át ezen a videón példákon is gyakorolva.
Gyakorló feladatok
Ebben a videóban a koordinátageometriai feladatok megoldását gyakorolhatod. Két hosszú, összetett feladat megoldását nézzük végig, amikben szinte minden koordinátageometriai összefüggés előkerül, amit már megtanultunk az előző videókon. Sőt, elemi geometriai tudásra is szükség van a példák megoldásához. Párhuzamos egyenesek, paralelogramma, metszéspontok koordinátái, kör egyenlete, Thálesz-tétel, pontok távolsága, háromszög területe - ezek mind-mind előkerülnek a példákban.
Felvételi feladatsor: 2006 M1 1-6. feladat
A 2006. évi felvételi feladatsor első hat feladatát nézzük át együtt: egyszerű, rövid műveletek, kombinatorikai feladat, szabályjáték, diagramok értelmezése, geometria, igaz vagy hamis, paralelogramma szögei, rombusz kerülete. (8.-os felvételi feladatsor, 6.-osoknak)
22. Területszámítás és integrálás ...
22. Tétel: Területszámítás elemi úton és az integrálszámítás felhasználásával. A tétel kifejtésében a területszámításról fogunk beszélni. Először elemi úton vizsgáljuk meg a témát, síkgeomatriai alakzatok területét részletezzük, majd áttérünk az integrálszámítás felhasználására. A tételt hallani fogod, és látni azt, amit közben érdemes a táblára írnod. Hogyan lehet definiálni egy alakzat területét? A területet úgy értelmezzük, mint egy függvényt, ahol minden síkidomhoz hozzárendelünk egy pozitív számot 3 tulajdonsággal. Ezek a következők: Az egységnégyzet területe 1. Az egybevágó sokszögek területe egyenlő. A 3. tulajdonság pedig úgy szól, hogy ha egy sokszöget feldarabolunk részsokszögekre, akkor a részek területének összege a sokszög területével egyenlő. Hogyan számoljuk ki különböző sokszögek területét? A sokszögek esetén a terület nagyságának meghatározása az egységnyi területtel való összevetés alapján történik. Ezt a szerepet tölti be az egységnégyzet. Nézzük át néhány speciális sokszög területének kiszámítási módját! A téglalap területe két szomszédos oldalának szorzatával egyenlő. A paralelogramma területe az egyik alap és a hozzátartozó magasság szorzata. Részletezzük a háromszög területének képletét, a trapéz területének kiszámítását. Mivel minden sokszög véges számú háromszögre darabolható, ezért a sokszög területe egyenlő a háromszögek területösszegével. A háromszög területének kiszámítására sok képlet van, ezek közül felírtam a leggyakrabban használtakat. Ezekben a képletekben s a félkerület, az r a beírt kör sugara, R pedig a háromszög körülírt körének a sugara. Azt a tételt bizonyítjuk, hogy átalános négyszög területét úgy számíthatjuk ki, hogy az átlók hosszát megszorozzuk a közre zárt szögük szinuszával, és ezt a szorzatot osztjuk kettővel. A bizonyítást a videón részletezzük. Szabályos sokszögek területét úgy kapjuk meg, hogy a középpontjukat összekötjük a csúcsokkal és így n db egyenlő szárú háromszöget kapunk, ezek területe már a középponti szög és a sugár ismeretében kiszámolható. Kör területének kiszámítása. Tétel: Az r sugarú kör területe r2pi-vel egyenlő. Mi a kapcsolat a területszámítás és az integrálszámítás között? A határozott integrállal függvénygörbe vonalával határolt síkidomok területét tudjuk meghatározni. A határozott integrál definíciójához szükségünk van még az intervallum felosztásának a definíciójára. Utána vesszük ennek a felosztásnak egy intervallumát, például az [xi-1;xi] zárt intervallumot. Kis mi legyen az f függvénynek ebben az intervallumban felvett értékeinek alsó határa, nagy Mi pedig a felső határa. Korlátos függvényeknél bizonyítható, hogy ezek az értékek léteznek. Az [xi-1;xi] intervallum fölé téglalapokat szerkesztünk, kettő darabot, kis mi, illetve nagy Mi magassággal. Ha ezt a felosztás összes intervallumában elvégezzük, megkapjuk a vizsgált tartomány egy körülírt és egy beírt sokszögét. Ezeknek a sokszögeknek vizsgáljuk meg a területét. A beírt sokszög területét alsó közelítő összegnek hívjuk, a körülírt sokszög területét pedig felső közelítő összegnek hívjuk. A felosztást finomíthatjuk. Így végtelen sok alsó és felső összeg keletkezik, amelyekről elmondható, hogy semelyik alsó összeg nem lehet nagyobb semelyik felső összegnél. Most már tudjuk definiálni a határozott integrált: Az [a; b] intervallumon korlátos, f függvény integrálható, ha bármely, minden határon túl finomodó felosztássorozatához tartozó alsó és felső összegei sorozatának közös határértéke van. Ezt a közös határértéket nevezzük az f függvény [a; b] intervallumon vett határozott integráljának. Két függvény által közrezárt síkidom területe is kiszámolható a határozott integrállal. Ha f(x)>g(x), akkor az f és g függvények görbéi által közrezárt síkidom területe az f – g függvény integrálásával számolható. A tételt matematika-történeti vonatkozások és gyakorlati alkalmazáshoz kapcsolódó példák zárják. A tétel végén pedig segítünk megtanulni is a tételt, gyakorolhatsz a saját tempódban.
18. Vektorok, vektorműveletek ...
18. tétel: Vektorok, vektorműveletek. Vektorfelbontási tétel. Vektorok koordinátái. Skaláris szorzat. A kidolgozott tételt fogod látni/ hallani a videón úgy, ahogyan azt a vizsgán is egy az egyben elmondhatod. Azokat érdemes felírni a táblára, amit a videón látsz kékkel. A videó 2. felében segítünk megtanulni is a tételt. Mit kell tudni a vektorokról? Az irányított szakaszokat nevezzük vektoroknak. A szakasz azért irányított, mert van kezdőpontja és végpontja. Ez egy szemléletes megoldás, a vektor alapfogalom, nem definiáljuk. Egy vektort két mennyiséggel lehet jellemezni, a hosszával és az irányával. A vektor abszolútértéke definíció szerint a vektort meghatározó irányított szakasz hosszát jelenti. A nulla hosszúságú vektort nullvektornak nevezzük. Ennek a vektornak az iránya tetszőleges. A tetszőleges irány annyit tesz, hogy mindig annyi, amennyi szükséges: a nullvektor lehet párhuzamos és merőleges is egy másik vektorhoz viszonyítva. Két nem nullvektor szöge 0°, ha egyirányúak, 180° ha ellentétes irányúak, más esetben a két vektor iránya által meghatározott két szög közül a kisebb. Milyen műveleteket végezhetünk vektorokkal, és hogyan? A vektorok között műveleteket értelmezünk. a és b vektor összege annak az eltolásnak a vektora, amellyel helyettesíthető az a vektorral és a b vektorral történő eltolások egymásutánja. A vektorösszeadás kommutatív és asszociatív művelet. Középiskolában vektorok összeadására a háromszög szabályt és a paralelogramma szabályt használtuk. Az a és b vektor különbségén azt a c vektort értjük, amelyre a = b + c teljesül. Ezzel ekvivalens az a definíció, hogy az a-hoz hozzáadjuk a b ellentettjét. Most ismertetem a vektor skalárral való szorzását. Egy nullvektortól különböző a vektor tetszőleges alfa valós számmal, azaz skalárral vett szorzata egy olyan vektor, amelynek abszolút értéke alfa*|a|; Az irána alfa > 0 esetén az a vektorral egyirányú; alfa
Vektorok - Műveletek vektorokkal
A vektorok irányított szakaszok. Először azokat a vektorokkal kapcsolatos ismereteket nézzük át, amelyekkel valószínűleg már találkoztál. Vektorműveleteket végzünk, vektorokat adunk össze és vonunk ki egymásból, vektort számmal szorzunk összefűzés, paralelogramma módszerével. Elmondjuk, mikor melyik módszert érdemes vagy kell alkalmazni.