Hatványozás azonosságai
Azonos alapú hatványokat úgy is összeszorozhatunk, hogy a közös alapot a kitevők összegére emeljük. ab · ac = ab + c
Azonos alapú hatványokat úgy is oszthatunk, hogy a közös alapot a kitevők különbségére emeljük.
Hatványt úgy is hatványozhatunk, hogy az alapot a hatványok szorzatára emeljük. ( ab ) c = ab · c
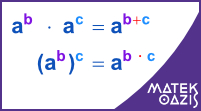
Azonos kitevőjű hatványokat úgy is szorozhatunk, hogy az alapok szorzatát a közös kitevőre emeljük. ab · cb = (a · c)b
Azonos kitevőjű hatványokat úgy is oszthatunk, hogy az alapok hányadosát a közös kitevőre emeljük.
Példák a hatványozás azonosságaira
Azonos alapú hatványok szorzása
53 ∙ 57 = (5 ⋅ 5 ⋅ 5) ⋅ (5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5) = 5(3+7) = 510
42 ⋅ 43 ⋅ 42 = (4 ⋅ 4) ⋅ (4 ⋅ 4 ⋅ 4) ⋅ ( 4 ⋅ 4) = 4(2+3+2) = 47
Azonos alapú hatványok osztása
Hatvány hatványozása
(52 )4 = 52 ⋅ 52 ⋅52 ⋅ 52 = (5 ∙ 5) ∙ (5 ∙ 5) ∙ (5 ∙ 5) ∙ (5 ∙ 5) = 5(2∙4) = 58
Azonos kitevőjű hatványok szorzása
23 ∙ 43 = (2 ∙ 2 ∙ 2) ∙ (4 ∙ 4 ∙ 4) = 2 ∙ 4 ∙ 2 ∙ 4 ∙ 2 ∙ 4 = (2 ∙ 4) ∙ (2 ∙ 4) ∙ (2 ∙ 4) = (2 ∙ 4)3 = 83
Azonos kitevőjű hatványok osztása
A következő Matek Oázis videókkal tanulhatsz a hatványozás azonosságairól
Hatványozás (ismétlés)
A hatványozás, a gyökvonás és a logaritmus összefüggenek egymással. A hatványozás az alapja mindennek, tehát nagyon fontos, hogy tisztában legyél ezek azonosságaival, és alkalmazni is tudd őket. Átismételjük a hatványozást egész kitevővel. Meghatározzuk a hatványozás definícióját, a hatványozás azonosságait. Feladatokat oldunk meg együtt a hatványozás gyakorlására.
2006. február / I. - 1-12. feladat
Ebben a matek tananyagban a 2006. februári matek érettségi feladatsor első 12 feladatának megoldásait nézzük át részletesen. Mértani sorozat, a hatványozás azonosságai, logaritmus-azonosságok, kombinatorika, valószínűség, algebra, gráfok, vektorok, százalékszámítás és halmazok -ezek a témakörök mind előkerültek a feladatokban.
2013-as felvételi feladatsor (Hangosítás nélkül)
A 2013. évi központi felvételi feladatsor. A feladatokat és a megoldásokat is megtalálod részletesen kidolgozva. Számolnod kell és mértékegységeket átváltani, táblázatot értelmezni. Szerepel a hatványozás, a százalékszámítás és a koordinátarendszer is. Meg kell oldanod szöveges és térgeometriai feladatot is.
2019. okt. 1-12. feladat
Oldjuk meg közösen a 2019-es októberi érettségi feladatsor első részét: gráfok, halmazok, hatványozás, százalékszámítás, számelmélet, függvények, geometria feladat szögfüggvények alkalmazásával, koordinátageometria, térgeometria és valószínűség. Sokféle témakör szerepel ebben a feladatsorban.
5. Hatványozás, gyökvonás ...
5. tétel : Hatványozás és a hatványfogalom kiterjesztése, a hatványozás azonosságai. Az n-edik gyök fogalma. A négyzetgyök azonosságai. Hatványfüggvények és a négyzetgyökfüggvény. A tétel kifejtésében először a pozitív egész kitevős hatványozásról, a művelet azonosságairól szeretnék beszélni, majd a hatványozás kiterjesztéséről először negatív egészekre, végül a valós számokra. Majd a hatványozás műveletének inverzéről, a gyökvonásról beszélek, a négyzetgyök azonosságairól, hatványfüggvényekről és négyzetgyökfüggvényről, végül ezek jellemző tulajdonságairól. Mi a hatványozás, hogyan értelmezzük pozitív egész számokra? A hatványozás két szám között értelmezett matematikai művelet. Jelölése Amennyiben az a pozitív egész szám, az an pontosan n db azonos, a-val jelölt szám szorzata. n = 1 esetén nem beszélhetünk szorzatról, definíció szerint minden szám első hatványa önmaga. A hatványozás azonosságai. Azonos alapú hatványokat úgy szorzunk össze, hogy az alap változatlan, ezt a kitevők összegére kell emelni. Azonos alapú hatványok hányadosa is velük azonos alapú hatvány lesz, a kitevőt pedig úgy kapjuk, hogy a számláló kitevőjééből kivonjuk a nevező kitevőjét. Ezek az azonosságok könynen igazolhatók a definíció alapján, a videón megmutatjuk, hogyan. A következő azonosság is hasonlóan bizonyítható, hatvány hatványozásakor a kitevők összeszorzódnak. Különböző alapú, de azonos kitevőjű hatványokkal is végezhetünk műveleteket. Ha összeszorozzuk őket, akkor megtehetjük, hogy először az alapokat összeszorozzuk, és csak utána hatványozzuk a szorzatot. Ez egyben azt is jelenti visszafelé, hogy a szorzatot tényezőnként is hatványozhatjuk. Ugyanígy a törtek esetében is a tört hatványa nem más, mint a számláló és a nevező megfelelő hatványának hányadosa. Mit jelent a negatív egész kitevőjű hatvány? A permanencia-elv alapján amennyiben nem a nullát hatványozzuk, bármely szám nulladik hatványát 1-nek definiáljuk. A negatív kitevőt is tudjuk értelmezni, tetszőleges nem nulla valós alap és n pozitív kitevő esetén az lesz. Hogyan értelmezzük, amikor racionális és irracionális szám van a hatvány kitevőjében? Egy a pozitív szám n/m-edik hatványa alatt azt a valós számot értjük, amelyet m. hatványra emelve az a n. hatványát kapjuk. Irracionális kitevőjű hatványt pedig azonos alapú, de racionális kitevős hatványok sorozatának határértékeként fogjuk fel. Igazolhatjuk, hogy az irracionális kitevős hatvány, mint határérték létezik, az azonosságok ugyanúgy érvényben maradnak. A gyökvonás műveletének definíciója. A gyökvonás a megfelelő értelmezési tartomány mellett a hatványozás inverz művelete. Egy nem negatív valós szám 2k-adik, azaz páros gyöke alatt azt a nemnegatív valós számot értjük, amelyet 2k-adik hatványra emelve az a nem negatív valós számot kapjuk vissza. A 2k+1-edik gyök műveletét valós számokon tudjuk végezni, 2k+1-edik gyöke egy valós számnak az a szám lesz, amelyet 2k+1. hatványra emelve az a számot kapjuk vissza. Fontos kapcsolat van a racionális törtkitevő és a gyökvonás között: n-edik gyök ( am) = an/m megfelelő értelmezési tartomány mellett, m pozitív egész szám. Racionális kitevő esetén nem értelmezzük, ha az alap negatív szám, hiszen akkor az m. gyök műveletének elvégzésénél problémák adódhatnának. A négyzetgyök és a köbgyök a két leggyakrabban alkalmazott művelet. A az a nemnegatív valós szám, amelyet önmagával megszorozva az a számot kapjuk vissza. A gyökvonás és a hatványozás művelete felcserélhető, ugyanez a helyzet akkor, ha negatív számról és páratlan gyökről van szó. Viszont ha a valós számok halmazán először emelünk páros kitevőre, majd ugyanennyiedik gyököt is vonunk, akkor a szám abszolútértékét kapjuk meg, nem negatív számok esetén magát a számot, negatív számok esetén pedig az ellentettjüket. A gyökvonás azonosságait ismertetjük. Az a és b nem negatív valós számok. Szorzatuk négyzetgyöke egyenlő a tényezők négyzetgyökének szorzatával. A tétel bizonyítását a videón részletezzük. További azonosságok: a nem negatív és pozitív valós számok estén a hányadosuk négyzetgyöke egyenlő a négyzetgyökeik hányadosával. Nem negatív alap esetén a hatványozás és a négyzetgyökvonás felcserélhető művelet, természetesen a 0 a nulladikon nincs értelmezve. A hatványfüggvényeket, és a tulajdonságaikat nézzük végig. Hatványfüggvénynek nevezzük azt a függvényt, melynek értelmezési tartománya a valós számok halmaza, a függvény x-hez az x n-edik hatványát rendeli hozzá, ahol n tetszőleges pozitív egész szám. Páros n-ek esetén a függvények grafikonja parabola alakú, egyre nagyobb hatvány esetén a parabola egyre szűkebb. Páratlan n-ek esetén pedig egy ilyen szép ívelt görbét kapunk, mivel negatív x-ek esetén a páratlan hatvány negatív lesz. A függvények jellemzésére is kitérünk, értékkészlet, páros/páratlan tulajdonság, monotonitás, szélsőérték, korlátosság, folytonosság, differenciálhatóság, integrálhatóság szempontjai alapján. Megnézzük azt is, hogyan változnak transzformált függvények esetén a függvény tulajdonságai. Mit kell tudni a négyzetgyökfüggvényről és tulajdonságairól? A négyzetgyökfüggvény a nemnegatív valós számok halmazáról képez le valós számokhalmazára, x-hez annak négyzetgyökét rendeli. Grafikonja egy fél fektetett parabola. A nemnegatív számok halmazán ez a függvény az függvény inverze. Értelmelmezési tartománya és értékkészlete a nemnegatív valós számok halmaza. További szempontok a függvényjellemzéshez: monotonitás, szélsőérték, korlátosság, folytonosság, differenciálhatóság, integrálhatóság. A hatványozás és a gyökvonás rengeteg helyen kap szerepet a feladatok megoldásában. Egyenletekben, geometriában, térgeometriában, Hasonlósági feladatok, egyéb geometriai számítások esetén gyakran kell hatványozni vagy gyököt vonni. Ugyanakkor a kamatos kamat számításnál, mértani sorozatoknál, számrendszerek, vagy akár a mértékváltás esetén is fontos.
23. Kombinációk, binom. tétel...
23. tétel: Kombinációk. Binomiális tétel, a Pascal-háromszög. A valószínűség kiszámításának kombinatorikus modellje. A hipergeometrikus eloszlás. A tételt kifejtve hallani fogod a videón, és közben megmutatjuk, mit érdemes a táblára írnod az emelt szintű szóbeli felelésnél. A tétel a témája a kombinatorika, és a valószínűségszámítás. Ezek véletlen tömegjelenségek törvényszerűségeivel foglalkoznak. Mik azok a kombinációk, és hogyan lehet kiszámolni őket? n elem k-ad osztályú ismétlés nélküli kombinációi: Legyen n egymástól különböző elemünk. Ha ezekből k darabot kiválasztunk minden lehetséges módon úgy, hogy a kiválasztott elemek sorrendjére nem vagyunk tekintettel, akkor n elem k-ad osztályú ismétlés nélküli kombinációit kapjuk. Azt a tételt bizonyítjuk, hogy az n elem k-ad osztályú ismétlés nélküli kombinációinak a számát az n alatt a k binomiális együttható adja meg. A binomiális együtthatók kiszámításának a módját is megnézzük a videón, és részletezzük a bizonyítást. Az ismétléses kombináció definíciója így szól: Ha n különböző elemből kell k db-ot kiválasztani úgy, hogy a kiválasztás sorrendje nem számít, és a már kiválasztott elemeket újra kiválaszthatjuk, akkor n elem k-ad osztályú ismétléses kombinációját kapjuk. Tétel mondja ki ezek számát, ez pedig éppen n+k-1 alatt a k. Miről szól a binomiális tétel? Egy kéttagú összeg hatványozására ad összefüggést a binomiális tétel: egy kéttagú összeget úgy is n-edik hatványra emelhetünk, hogy összeadjuk a két tag összes olyan hatványának szorzatát, melyben a hatványok kitevőinek összege a kéttagú összeg kitevője, azaz n. Ezt megszorozzuk egy binomiális együtthatóval, mégpedig a Pascal-háromszög n-edik sorának annyiadik elemével, ahányadaik hatványon az első tag áll a szorzatokban Fontos megemlíteni, hogy a Pascal-háromszögben a sorok és a sorok elemeinek számozását is a 0-tól kezdjük. Milyen tulajdonságai vannak a binomiális együtthatóknak? A binomiális együttható két tulajdonságát ismertetem most: Mivel 0! definíció szerint 1-el egyenlő, ezért n alatt a 0 és n alatt az n is 1-gyel egy. A második tulajdonság, hogy az n elem közül k darabot és n-k darabot is ugyanannyi-féleképpen lehet kiválasztani. Tehát n alatt a k és n alatt az n-k egyenlők. Az eddig ismertetett definíciók és tételek segítségével megoldhatunk olyan kiválasztási problémákat, mint például hogy hányféleképp lehet kitölteni egy ötöslottó szelvényt. Vagy például ki tudjuk számolni, hogy egy n elemű halmaznak hány darab k elemű részhalmaza van. Mi a Pascal háromszög? Hogyan számíthatjuk ki az elemeit? A Pascal háromszög lényegében a binomiális együtthatók háromszög alakban való elrendezése. Ahogy már említettem a sorok számozása nullával kezdődik. A páros számú és páratlan számú sorokban a számok el vannak csúsztatva egymáshoz képest. A háromszög felírása nem nehéz, az első sorba csupán egy egyest kell írni. A következő sorok felírásánál a szabály a következő: az új számot úgy kapjuk meg, ha összeadjuk a felette balra és felette jobbra található két számot. Az n. sor k. elemének kiszámítására a képletet a háromszög névadója, a francia matematikus Pascal adta meg. A Pascal háromszög n-edik sorában a kéttagú összeg n-edik hatványának együtthatói, azaz a binomiális együtthatók állnak. Mit jelent a valószínűségszámítás kombinatorikai modellje? . A valószínűségszámítás axiómái: 1.) Tetszőleges A esemény valószínűsége nagyobb vagy egyenlő mint 0 és kisebb vagy egyenlő, mint 1. 2.) Biztos esemény valószínűsége 1, lehetetlen esemény valószínűsége 0. 3.) Ha A és B egymást kizáró események, akkor a valószínűség így is számolható: P(A+B) = P(A) + P(B) A esemény valószínűsége és A esemény komplementerének a valószínűsége együtt 1-el egyenlő. Mi a hipergeometrikus eloszlás és hogyan számolhatjuk ki? Most áttérnék a diszkrét eloszlásokon belül a hipergeometrikus eloszláshoz. Ehhez definiáljuk először a valószínűségi változót, majd a hipergeometrikus eloszlást, és elmondjuk annak jellemzőit, és megmutatjuk a kiszámításának módját. A hipergeometrikus eloszlás várható értékét is felírjuk. Matematikatörténeti vonatkozásokra is kitérünk a tétel kifejtése közben.
Egész számok szorzása, osztása, hatványozása
Pozitív és negatív egészek szorzását, osztását gyakoroljuk pozitív és negatív egész számokkal. Hogyan változnak az előjelek? Megvizsgáljuk a hatványozást is a pozitív és negatív egész számok terén. Mi történik páros és páratlan számú negatív tag szorzata esetén? Figyelj a műveleti sorrendre!
n-edik gyök, törtkitevős hatvány
A mostani matekvideóban először is az n-edik gyök fogalmát ismételjük át, példákkal, foglalkozunk a páros és páratlan gyök közötti különbségekkel. Aztán megnézzük, mit jelent az, ha a hatvány kitevőjében egy törtszám áll. Majd megmutatjuk, hogy így egyesítve a gyökvonást a hatványozással, mennyivel könnyebb a törtkitevőkkel műveleteket végezni.