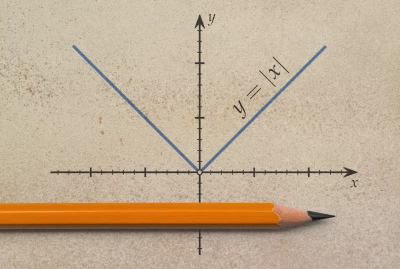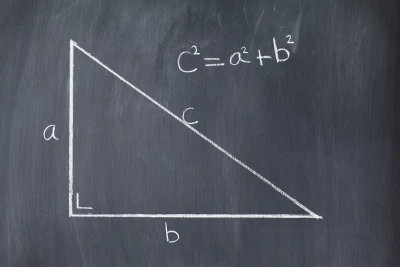Matematika 9. osztály
A teljes 9.-es matek
Kombinatorika, gráfok, halmazok, skatulyaelv
1. Kombinatorika, gráfok
2. Halmazok, intervallumok
3. Skatulyaelv
Műveletek, arányosság, százalék
4. Műveletek
5. Arányosság, százalék
Szöveges feladatok
6. Szövegesek megoldása, típusfeladatok
Algebra
7. Algebra alapozó (ism.)
8. Hatványozás, gyökvonás - alapok (ism.)
9. Hatványozás, normálalak
10. Algebrai kifejezések, nevezetes azonosságok
Egyenletek, egyenlőtlenségek, egyenletrendszerek
11. Egyenletek
12. Egyenlőtlenségek
13. Egyenletrendszerek
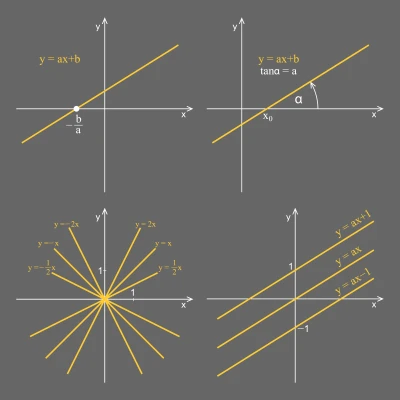
Függvények
14. Alapok
15. Függvénytípusok, gyakorlás
16. Függvények jellemzése, transzformációi
Statisztika
17. Alapfogalmak, grafikonok értelmezése, készítése
Geometria
18. Háromszögek
19. Négyszögek, sokszögek, kör
20. Geometriai transzformációk
Évvégi ismétlő feladatsorok
21. Ismétlés
Számelmélet, számrendszerek --> Az aktuális Nemzeti Alaptanterven túlmutató tananyagok
22. Oszthatóság, lnko, lkkt, számrendszerek
Nem találod amit keresel?

Tisztelt Szerkesztő! Az interneten rátaláltam az Ön által szerkesztett programra. Nagyon jónak találom. A gyermekem még csak 9. osztályba jár, tehát nem érettségire készül. Sajnos gondjai vannak a matematikával. Nekem tanító a végzettségem, de már régen foglalkoztam gimnáziumi tananyag megoldásával. Sem a gyermekem tankönyve, sem pedig az órai munkák áttanulmányozása nem nyújt kellő segítséget a megértéshez és a feladat elmagyarázásához. Ezzel szemben az Ön anyaga világos, könnyen megérthető és megértethető.
Gizella
Kedves Beáta! ... A gyerekeim számára rendeltem meg a videót, nagyon sokat segít nekik a Ti munkátok. Iker gyerekeim vannak, egy lány és egy fiú. A Ti segítségetekkel készültünk a középiskolai központi írásbelire és most a 9. évfolyam anyagával segítem őket a matekban. Sajnos kevés jól magyarázó matektanár van. El sem tudom mondani, milyen nagy öröm számomra, amikor a Ti magyarázatotok után végre kimondják, hogy "értem, nem is olyan nehéz". Köszönöm a munkátokat, az eddigi lehetőségeket és további sikeres munkát kívánok! Üdvözlettel:
Horváth Zsuzsanna
Kedves Tanárnő, Kedves B. Békési Beáta, Szeretnénk köszönetet mondani a videókról, illetve a honlapról kapott segítségért. A gimnázium első éve (9. osztály) nagyon riasztó (egyes, kettes) matek-jegyekkel kezdődött, és a gyakorlásnak hála, most már négyesekkel folytatódik, sőt ötösök is be-becsúsznak. Nagyon köszönjük! A legjobbakat kívánjuk, üdvözlettel,
Blaticzky Anna és családja
Múlt hónapban rendeltem meg a 9. osztályos matematikai csomagot. Nagyon tetszik a gyereknek és egy jeggyel jobbat írt. Meg vagyok elégedve vele.
Balog Tamásné
Ha neked is meggyűlt a bajod a matekkal, akkor lehet, hogy általánosból hoztál olyan hiányosságokat, amik most visszaütnek, de az is lehet, hogy nehezen alkalmazkodsz az új tanárhoz. Ne aggódj, ez a matek is megtanulható! Ha akarod, segítünk. Próbáld ki az ingyenes videókon, milyen könnyű és érthető így a matek! B. Békési Bea
A szerethető matektanulás szakértője
Matektanár
Szeretnéd, ha gyermeked nem csak a matekban, hanem az élet minden területén sikeresebb lenne?
LOGIKA kurzusunk játékos és interaktív módon segít gyermekednek fejleszteni a kritikus gondolkodását és a problémamegoldó képességét, amelyek egy életre szóló előnyt jelentenek.