Matematika érettségi 2021 feladatok: ezek voltak a feladatok a megoldásokkal együtt!
Milyen feladatok voltak? | Megoldás I. (interaktív) | I. rész feladatai | Megoldás II. (interaktív) | II. rész feladatai
A 2021-es matematika érettségi nem okozott nagy meglepetéseket a diákoknak. De ez nem jelenti azt, hogy ne lett volna nehéz az érettségizőknek.
Most már évek óta tendencia, hogy nemcsak az I. rész versenyfutás, hanem a II. rész megoldása közben is igencsak gyorsan kell dolgozni. Sok a részkérdés, sokkal több a részfeladat, mint pár évvel ezelőtt. Olyan feladatokra, amikre 5 éve még megadták a 12-13 pontot, ma már csak a fele jár, a másik feléért újabb kérdés(ek)re kell válaszolni.
Matematika érettségi 2021: milyen feladatok voltak?
Egy gyors áttekintés, hogy milyen témakörből hány pontot lehetett szerezni:
Meglepetés volt, hogy a hagyományosnak számító matematika témakörök kerültek abszolút túlsúlyba a 2021-ben:
1. helyezett: Egyenletek (és algebra) 22 pont (!)
2. helyezett: Síkgeometria 18 pont
és ezt mind a kötelező részekből!!
3. Százalékszámítás (- szövegesekben) 12 pont (ebből 8 pont az 1.-15. feladatokból)
4. Sorozatok 10 pont
5. - 6. Koordinátageometria és Függvények 9 – 9 pont
7. - 8. Kombinatorika; Valószínűségszámítás 8 - 8 pont (az előző évek tapasztalata után ennél sokkal többet vártunk…)
9. Térgeometria 7 pont
10. Gráfok 6 pont
További témakörök:
Statisztika (4 pont); Halmazok, oszthatóság (2 pont); Logika (2 pont)
Nézzük részletesen a feladatokat – megoldásokkal együtt!
Itt megtalálod a 2021-es matematika érettségi I. részének feladatait interaktív megoldásokkal, amikből nagyon sokat tanulhatsz:
Hasonló interaktív videókon átnézhetsz minden matek érettségi témakört, és begyakorolhatod az érettségi feladatok megoldását:
Megnézem az érettségi tréning részleteit
1. Egy számtani sorozat második tagja 8, negyedik tagja 18.
Határozza meg a sorozat első tagját! (2 pont)
2. Hányadik hatványra kell emelni a 2-t, hogy 512-t kapjunk? (2 pont)
3. Legyen A a pozitív, kétjegyű páros számok halmaza, és B pedig a 40-nél kisebb, 3-mal osztható pozitív számok halmaza.
Elemei felsorolásával adja meg az A ∩ B halmazt! (2 pont)
4. Egy négyszög belső szögeinek aránya 1 : 2 : 3 : 4. Hány fokos a négyszög legnagyobb szöge?
Válaszát indokolja! (4 pont)
5. Válassza ki az alábbiak közül az összes állítást, amely tagadása a következőnek!
„Volt olyan nap a múlt héten, amikor esett az eső.”
A: A múlt héten minden nap esett az eső.
B: A múlt héten egyik nap sem esett az eső.
C: Nem volt olyan nap a múlt héten, amikor esett az eső.
D: Volt olyan nap a múlt héten, amikor nem esett az eső. (2 pont)
6. Egy diákmunka-közvetítéssel foglalkozó cég 25 állást hirdetett meg.
Az állások órabérét és ezek gyakoriságát az alábbi táblázat tartalmazza.
Adja meg a hirdetésekben szereplő órabérek terjedelmét, móduszát, mediánját és átlagát!
| Órabér (Ft) | 1000 | 1200 | 1500 | 1600 |
| Állások száma (db) | 9 | 4 | 5 | 7 |
(4 pont)
7. Ha egy egészségpénztári számlára befizetünk egy összeget, akkor abból először levonnak
6% működési költséget, és a fennmaradó összeget írják jóvá a számlán.
Hány forintot írnak jóvá a számlán 150 000 Ft befizetése esetén? (2 pont)
8. A derékszögű koordinátarendszerben ábrázoltuk a valós számok halmazán értelmezett
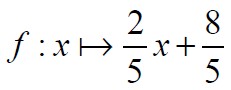
függvényt. Adjon meg egy olyan pontot a koordinátáival, amely illeszkedik
a függvény grafikonjára! (2 pont)
9. Egy szabályos sokszög egyik csúcsából behúztunk két átlót, így a sokszöget egy háromszögre, egy négyszögre és egy ötszögre bontottuk.
Hány oldalú a szabályos sokszög? (2 pont)
10. Oldja meg az alábbi egyenletet a valós számok halmazán!
|x-4|=1 (2 pont)
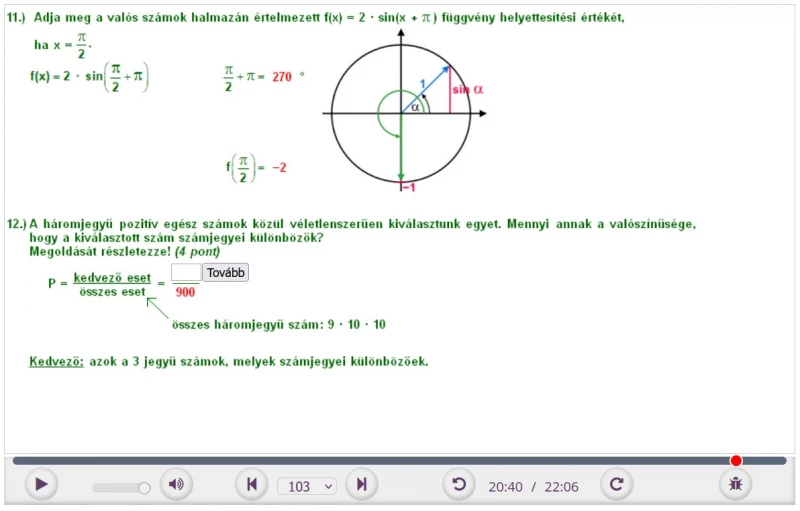
11. Adja meg a valós számok halmazán értelmezett f (x) = 2 ∙ sin(x + π) függvény helyettesítési értékét, ha x = π/2 . (2 pont)
12. A háromjegyű pozitív egész számok közül véletlenszerűen kiválasztunk egyet.
Mennyi annak a valószínűsége, hogy a kiválasztott szám számjegyei különbözők?
Megoldását részletezze! (4 pont)
Megnézem az érettségi tréning részleteit
A nehezebb feladatok és megoldásaik:
A matematika érettségi II. részének feladatai (13-15. feladat) »
Az interaktív megoldásokhoz jelentkezz be!
A matematika érettségi II. részének feladatai (16-18. feladat) »
Az interaktív megoldásokhoz jelentkezz be!
A 2021. érettségi feladatok II. része:
13.
a) Oldja meg az alábbi egyenletet a valós számok halmazán!
(x + 4)2 + (x +1) ⋅(x + 2) = 9
b) Oldja meg az alábbi egyenletrendszert a valós számpárok halmazán!
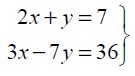
(12 pont)
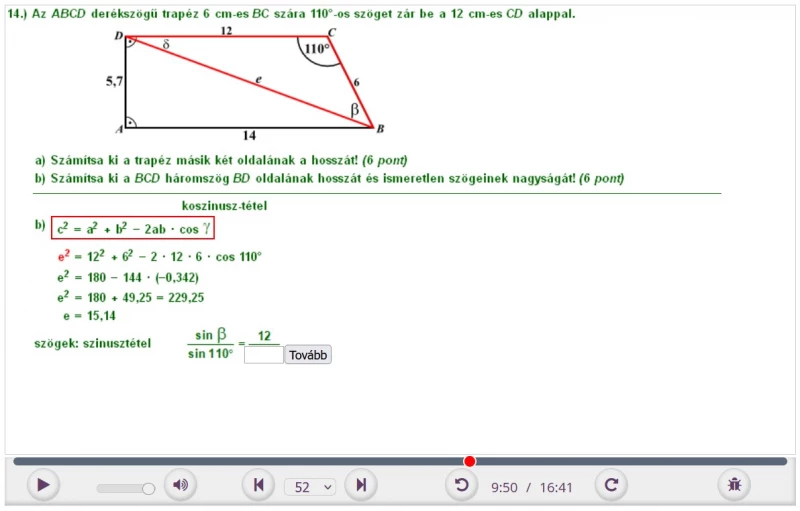
14. Az ABCD derékszögű trapéz 6 cm-es BC szára 110°-os szöget zár be a 12 cm-es CD alappal.
a) Számítsa ki a trapéz másik két oldalának a hosszát!
b) Számítsa ki a BCD háromszög BD oldalának hosszát és ismeretlen szögeinek nagyságát!
15.
Amerikai kutatók 104 labrador genetikai elemzése alapján felállítottak egy egyenletet,
amellyel (a kutya 3 hónapos korától) megmondható, milyen korú az adott kutya emberévekben.1 A kutya valódi életkorát években mérve jelölje K, ekkor az emberévekben
kifejezett életkort (E) az alábbi képlettel kapjuk: E = 37 ⋅ lg K + 31 (ahol K > 0,25).
a) Egy kutya emberévekbe átszámított életkora E = 70 év.
Hány év, hány hónap ennek a kutyának a valódi életkora?
Válaszát egész hónapra kerekítve adja meg!
Egy másik átszámítás szerint – a kutya 3 éves korától kezdve – az emberévekben kifejezett
életkor az e = 5,5 ⋅ K + 12 képlettel kapható meg (ahol K > 3).
b) Számítsa ki egy K = 8 éves labrador esetén az emberévekben kifejezett életkort
mindkét képlettel!
Az amerikai kutatók képletéből kiszámított érték hány százalékkal nagyobb, mint a
másik képletből kiszámított érték?
(12 pont)
16.
Egy nyolccsapatos jégkorongbajnokságban minden csapat minden másikkal egyszer mérkőzik meg.
Az ábrán látható gráf az eddig lejátszott mérkőzéseket szemlélteti. A pontok a csapatokat jelképezik, és két pont között pontosan akkor van él, ha a két csapat már játszott egymással.
A bajnokságból 5 fordulót már megrendeztek, ám néhány mérkőzés elmaradt. (Egy fordulóban – ha nincs elmaradó mérkőzés – mindegyik csapat egy mérkőzést játszik.)
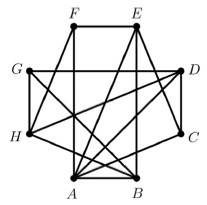
a) Adja meg három olyan csapat betűjelét, melyek közül bármely kettő már lejátszotta
az egymás közötti mérkőzését!
b) Hány mérkőzés maradt el az első 5 fordulóban?
Az egyik játékos 0,3 valószínűséggel szerez gólt egy büntetőlövésből.
c) Mekkora a valószínűsége, hogy 10 büntetőlövésből pontosan 4 gólt szerez?
A szabványos jégkorong egy olyan vulkanizált gumihenger, amelynek magassága 2,54 cm (1 inch), alapkörének átmérője 7,62 cm (3 inch). Az egyik csapat a pálya bejáratához egy olyan négyméretű
korongot terveztet, amely (matematikai értelemben) hasonló a szabványos jégkoronghoz. A tervben szereplő négyméretű korong térfogata 1 m3.
d) Számítsa ki a négyméretű korong magasságának és alapköre átmérőjének a hosszát!
(17 pont)
17. a) Az x mx + b lineáris függvény 1-hez 200-at, 21-hez pedig 5200-at rendel.
Adja meg m és b értékét!
Anna szeretne részt venni a Balaton-átúszáson, amelyhez két különböző 21 napos edzéstervet készít. Azt már elhatározta, hogy az első napon 200 métert, az utolsó, 21. napon pedig az átúszás teljes távját, 5200 métert úszik. Az egyik edzéstervben a napi úszásmennyiségek egy számtani sorozat egymást követő tagjai, a másik változatban pedig (jó közelítéssel) egy mértani sorozaté.
b) A teljes felkészülés alatt összesen hány métert úszna Anna az egyik, illetve a másik változatban?
A 2020-as Balaton-átúszáson az indulók 36%-a volt nő, átlagéletkoruk 35 év. Az indulók 64%-a volt férfi, átlagéletkoruk 38 év.
c) Mennyi volt ebben az évben az összes induló átlagéletkora?
(17 pont)
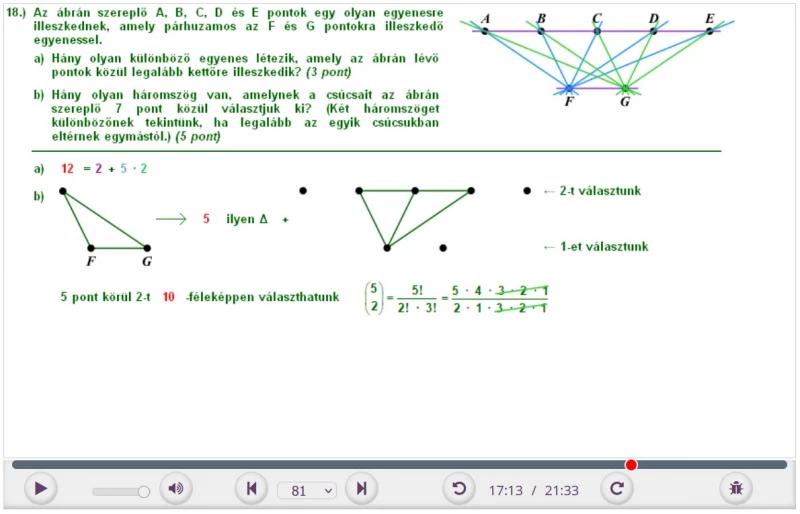
18. Az ábrán szereplő A, B, C, D és E pontok egy olyan egyenesre illeszkednek, amely párhuzamos az F és G pontokra illeszkedő egyenessel.
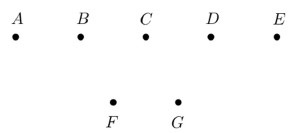
a) Hány olyan különböző egyenes létezik, amely az ábrán lévő pontok közül legalább kettőre illeszkedik?
b) Hány olyan háromszög van, amelynek a csúcsait az ábrán szereplő 7 pont közül választjuk ki? (Két háromszöget különbözőnek tekintünk, ha legalább az egyik csúcsukban eltérnek egymástól.)
Egy háromszög csúcsai: K(– 1; 5), L(1; 1), M(5; 3).
c) Igazolja, hogy a háromszög L-nél lévő szöge derékszög!
d) Írja fel a háromszög körülírt körének az egyenletét!
(17 pont)
A feladatokat és a megoldókulcsot innen letöltheted:
(forrás: OM)

Ha sok hiányosságod van még, az intenzív tréninggel bepótolhatod, és egy klassz érettségit írhatsz:
Hihetetlenül gyorsan tudsz fejlődni matekból az egyedi módszereknek és a jól felépített tananyagnak köszönhetően:
Megnézem az érettségi tréning részleteit

A szerethető matektanulás szakértője, matektanár
TAVASZI KIHÍVÁS
Gyűjts csillagokat és nyerj akár egy Apple iPad-et!
Vagy a többi menő nyeremény egyikét
BENEVEZEK »