Viéte-formulák
Egy másodfokú, nullára redukált egyenlet általános alakja: .
A Viéte-formulák az egyenlet gyökei (x1 és x2 megoldások) és együtthatói ( a, b, c) közötti össszefüggések:
és
Jól látszik, hogyha x2 együtthatója 1 (azaz a = 1), akkor akár az egyenlet megoldásához is könnyű használni a Viéte-formulákat.
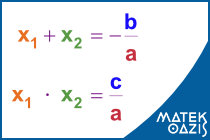
Példák a Viéte-formulák alkalmazására
1. Feladat: Oldjuk meg megoldóképlet nélkül az x2 + 4x - 5 = 0 egyenletet!
Megoldás: Használjuk a VIéte-formulákat! Az egyenlet két megoldása x1 és x2. Az együtthatók pedig a = 1; b = 4; c = -5. A két gyök összege -b-vel egyenlő, azaz
Felírjuk a másik formulát is:
Tehát olyan számpárt keresünk, amiknek az összege -4, a szorzatuk pedig -5. Ilyen számpár egy van: x1 = 1 és x2 = -5 vagy fordítva.
2. Feladat: Írjunk fel olyan másodfokú egyenletet, amelynek gyökei 9 és -2!
Megoldás: Megint használjuk a Viéte-formulákat!
Ha az a együtthatót 1-nek vesszük, akkor -b = 7 miatt b = -7-et kapunk, a második összzefüggésből pedig c = -18. Így felírhatunk egy megfelelő egyenletet: x2 - 7x - 18 = 0
A következő Matek Oázis videókkal tanulhatsz a Viéte-formulákról
Másodfokú egyenletek
A másodfokú egyenletek megoldásánál a legfontosabb, hogy ismerd és alkalmazni tudd a másodfokú egyenlet megoldóképletét. A diszkrimináns ismerete segíthet a gyökök számának meghatározásában. Tudni kell a Viete-formulákat is, a gyökök és együtthatók közötti összefüggéseket. Mindezeket megtanulhatod, és begyakorolhatod ezzel a videóval.
7. Másodfokú egyenletek, egyenlőtlenségek
7. tétel: Másodfokú egyenletek és egyenlőtlenségek. Másodfokúra visszavezethető egyenletek. Egyenletek ekvivalenciája, gyökvesztés, hamis gyök, ellenőrzés. Megmutatjuk a teljes kidolgozott tételt, úgy, ahogyan a vizsgán elmondhatod. Közben látni fogod, hogy mit érdemes a táblára írni. A videó második felében segítünk, hogy gyorsan meg is tudd tanulni a tételt. Mi az egyenlet, mit jelent az egyenlet alaphalmaza, értelmezési tartománya, illetve az egyenlet megoldásai? Ha két algebrai kifejezést egyenlőségjellel kapcsolunk össze, egyenletet kapunk. Az egyenlet leírásában egy vagy több változó szerepel. Az egyenlet megoldása során a változónak vagy változóknak azokat az értékeit keressük meg, amelyekre az egyenlet igaz logikai értéket vesz fel. Ez(ek) az egyenlet megoldásai vagy gyökei Minden egyenletnek van egy alaphalmaza, és ennek egy részhalmaza az értelmezési tartomány. Az értelmezési tartomány az alaphalmaznak azon legbővebb részhalmaza, amelyen az egyenletben szereplő összes algebrai kifejezés értelmezve van. Amennyiben nem adunk meg mást, a valós számok halmazát tekintjük alaphalmaznak. Ha az értelmezési tartomány minden elemére igaz lesz az egyenlet, akkor azt mondjuk, hogy az az egyenlet azonosság. Ha egyetlen értelmezési tartománybeli elemre sem igaz az egyenlet, akkor az egyenletnek nincs megoldása. Egy másik megközelítés szerint az egyenlet mindkét oldala egy-egy függvény hozzárendelési szabálya. Az egyenlet megoldása során pedig azokat az értelmezéstartománybeli -eket keressük, amelyekre a két függvény felvett függvényértéke megegyezik. Amennyiben grafikus úton oldjuk meg az egyenletet, a két függvény metszéspontjának vagy metszéspontjainak koordinátája lesz a keresett megoldás. Melyek a másodfokú egyenletek, és hogyan oldjuk meg őket? A másodfokú egyenletek kanonikus, vagy nullára rendezett alakja: ax2 + bx + c = 0 alakú, ahol a, b és c valós paraméterek. Ők az úgynevezett együtthatók, x pedig a változó. Az a értéke nem lehet 0, hiszen akkor nem lenne x2 -es tag, tehát az egyenlet nem lenne másodfokú. Tétel: ax2 + bx + c = 0 alakú, (a nem 0) másodfokú egyenlet megoldásait az x1,2 =…. (másodfokú egyenlet megoldóképlete) képlettel kaphatjuk meg. A bizonyítás lépéseit a videón láthatod. A másodfokú egyenlet megoldásainak a száma a diszkriminánstól függ. A diszkrimináns a megoldóképletben a gyök alatt látható kifejezés. Ha D < 0, nincs valós gyök, ha D = 0, két egybeeső valós gyök van, ha D > 0, két különböző valós gyök van. Feladat: x2 + 6x + 8 = 0 egyenletet megoldjuk a megoldóképlettel. Hogyan kell megoldani paraméteres másodfokú egyenleteket? Paraméteres másodfokú egyenletek esetén gyakran a paramétert a gyökök számára vagy tulajdonságára megadott adat alapján kell meghatározni. Példa: px2 + 4x + p = 0 egyenletben p a paraméter, x az ismeretlen. Ha pl. az a kérdés, hogy a p paraméter milyen értékei mellett lesz egy megoldása ennek az egyenletnek, akkor ezt a diszkrimináns vizsgálatával lehet megválaszolni. D = 0 -ból kapunk p-re egy összefüggést, annak a megoldásait kell keresni. Gyökök és együtthatók közötti összefüggések felírása, gyöktényezős alak, Viete-formulák. Ha az ax2 + bx + c = 0 másodfokú egyenletnek létezik valós gyöke, akkor a másodfokú kifejezés elsőfokú tényezők szorzatára bontható a gyöktényezős alak segítségével. ax2 + bx + c = a ( x - x1 )( x - x2 ) A Viete-formulák a gyökök és együtthatók közt teremtenek kapcsolatot: x1 + x2 = -b/a ; és x1*x2 = c/a A Viete-formulákat és a gyöktényezős alakot is könnyen igazolhatjuk, ha az x1 -re és x2 -re kapott megoldóképletet behelyettesítjük az összefüggésekbe. A Viete-formulák és a gyöktényezős alak is számos feladat megoldását könnyíti meg. Például nem negatív diszkrimináns esetén szorzat alakba tudjuk írni a másodfokú számlálót vagy nevezőt, így egyszerűsíteni tudunk az azonos tényezőkkel. A másodfokú egyenlőtlenség megoldásának lépései. Ha másodfokú egyenlőtlenséget akarunk megoldani, akkor általában grafikus módon fejezzük be a feladatmegoldást, miután a megoldóképlettel a gyököket meghatároztuk. A másodfokú hozzárendelés képe parabola, a kiszámított gyökök a parabola zérushelyei. Két egybeeső valós gyök esetén a parabola érinti az x tengelyt, ha nincs valós gyök, akkor pedig a másodfokú kifejezés minden x-re pozitív vagy minden x-re negatív értéket vesz fel. A parabola ábrázolása után az egyenlőtlenség megoldásai leolvashatók a garfikonról. Melyek a másodfokúra visszavezethető egyenletek és hogyan oldjunk meg őket? Ha egy kifejezés és ugyanannak a kifejezésnek a négyzete szerepel az egyenletben, akkor az adott kifejezésre érdemes új ismeretlent bevezetünk. Mert így az új ismeretlenre nézve lesz másodfokú az egyenlet vagy az egyenlőtlenség. Ezek az egyenletek, egyenlőtlenségek eredeti formájukban lehetnek például magasabb fokúak, logaritmusosok, trigonometrikusak vagy akár összetettebb algebrai kifejezésre nézve másodfokúak. Megnézünk néhány példát is. Mikor ekvivalens az egyenlet átalakítása? Mikor fordulhat elő gyökvesztés illetve hamis gyök? Miért és mikor kell ellenőrizni az egyenlet megoldását? Nagyon fontos, hogy az egyenletek, egyenlőtlenségek megoldásánál mindig figyeljük, hogy ekvivalens, vagy nem ekvivalens a végrehajtott lépés, vagyis azt, hogy a lépések következtében az újabb és újabb egyenlet ekvivalens-e az előző lépésben szereplő egyenlettel. Két egyenlet akkor ugyanaz, ha értelmezési tartomány a és megoldáshalmaza is ugyanaz. Ekvivalens átalakításokra és nem ekvivalensekre is mutatunk példákat. Ha az átalakítás során megváltozik az egyenlet értelmezési tartománya, gyököt veszíthetünk, de akár hamis gyökök is jöhetnek be. A hamis gyököket lehet kizárni ellenőrzéssel. A másodfokú egyenletek, összefüggések alkalmazására mutatunk példákat a tétel végén.
Másodfokú egyenletek gyakorlása 1.
Ezen a videón sok szép gyakorló feladatot találsz. Miután a korábbi videón már megmutattuk, hogyan kell alkalmazni a másodfokú egyenlet megoldóképletét, mi az a diszkrimináns, és hogy a Viete-formulák tulajdonképpen a másodfokú egyenlet gyökei és együtthatói közötti összefüggések, ezek a feladatok már biztos nem fognak gondot okozni.
2025. május 4-6. feladat emelt szintű matek érettség
Emelt szintű matematika érettségi 2025. . Folytatjuk az emelt szintű érettségi feladatok megoldását a 4-6. példákkal Koordinátageometria: kör egyenlete, parabola egyenlete. A 4. feladat első felében a kör egyenletével kell dolgoznunk, illeszkedés, tengelymetszet és egyebek kerülnek terítékre. A b) részben a parabola egyenletével számolunk. Parabola tengelypontja és paramétere is szerepel a feladatban. Egyenletrendszer, valószínűségszámítás, statisztika. Az 5. feladat igazi vegyes példa. Megoldunk egy nehezebb egyenletrendszert, majd egy középszintű valószínűségszámítással folytatjuk. A feladatot egy sodrófa-diagram zárja. Függvények, integrálás, analízis. A 6. feladat elején egy halmazokkal tarkított függvényes feladattal találkozunk, végül deriválással és integrállással zárjuk a videót.