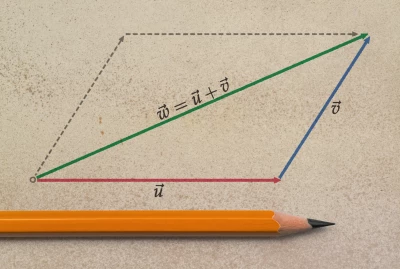
Vektor szorzása számmal

Legyen a (a1 ; a2) vektor és lambda(lamda) valós szám. Ha egy vektort megszorzunk egy valós számmal (skalárral), akkor a vektor hossza |lambda| -szorosára változik, az iránya pedig marad ugyanaz, ha a szám pozitív, vagy ellenkezőjére változik, ha  a szám  negatív. 

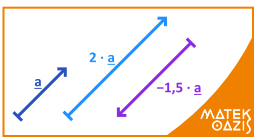
vektor szorzása számmal

Koordinátáival adott vektor esetén nagyon egyszerű a számmal való szorzás: a vektor minden koordinátáját szorozni kell a számmal:

lambda times bottom enclose a equals left parenthesis lambda times a subscript 1 space semicolon space lambda times a subscript 2 right parenthesis

Példa a vektor számmal való szorzásának megértéséhez

Feladat: Adott a (7 ; -2) vektor és lambda = 5. Végezzük el lambda times bottom enclose a szorzást!

Megoldás: lambda times bottom enclose a equals left parenthesis lambda times a subscript 1 space semicolon space lambda times a subscript 2 right parenthesis equals left parenthesis 5 times 7 space semicolon space 5 times left parenthesis negative 2 right parenthesis right parenthesis equals left parenthesis 35 space semicolon space minus 10 right parenthesis

A kövekező Matek Oázis videókkal tanulhatsz a vektor számmal való szorzásáról

Nincs találat