Téglalap
A téglalap egy olyan négyszög, aminek minden szöge 90°-os, azaz derékszög.
A téglalap szemközti oldalali egyenlő hosszúságúak (két a hosszúságú oldal és két b hosszúságú oldal)
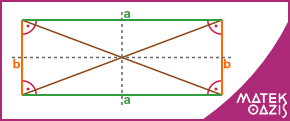
A téglalap átlói egyenlő hosszúak és felezik egymást.
Tengelyesen és középpontosan is szimmetrikus négyszög.
Ha egy téglalap minden oldala egynelő hosszúságú, akkor az négyzet. (Emiatt minden négyzet téglalap, de nem minden téglalap négyzet.)
A téglalap kerülete: K = a + b + a + b = 2 · (a + b). A téglalap területe: T = a · b
Feladat a téglalap tulajdonságairól
Feladat: Döntsük el a következő állításokról, hogy igaz vagy hamis!
a) Ha egy téglalap átlói egyenlő hosszúak, akkor a téglalap négyzet.
b) Ha egy téglalapnak két szomszédos oldala egyenlő hosszú, akkor ez a téglalap négyzet.
c) Ha egy téglalap átlói felezik egymást, akkor a téglalap négyzet.
Megoldás:
a) Az állítás hamis. Bármelyik téglalapnak egyenlő hosszúak az átlói, nem csak az a négyzetnek. Például: ha a = 3 cm és b = 10 cm, akkor is egyenlő hosszúak az átlók.
b) Az állítás igaz. Eszerint ha az a oldal és a szomszédos b oldal is egyenlő hosszú, akkor mind a négy oldal egyenlő hosszúságú, mert a téglalap szemközti oldalai egyenlő hosszúságúak.
c) Az állítás hamis. Minden téglallap átlói felezik egymást, akkor is, ha eltérő hosszúságúak a szomszédos oldalak.
A következő Matek Oázis videókkal tanulhatsz a téglalapról
2017/I. feladatsor 1-6. feladat
Oldjuk meg közösen a 2017. évi I. feladatsor 1-6. feladatát: műveletvégzés törtekkel, tizedestörtekkel, mértékegység váltások, adatok értelmezése, számok helyiértéke, kerekítés, sorozatok képzése, négyzet-téglalap kerülete és területe, ez mind hosszú és bonyolult szöveges példákban.
Területszámítás
JÁTÉK! Építsd fel és rendezd be a babaházat! Számítsd ki a téglalapok és négyzetek területét, és hasonlítsd össze őket egymással vagy a megadott számmal! Kattints a helyes relációs jelre, és látni fogod a magyarázatot is. Ügyelj a mértékegységekre is! Mire a babaház felépül, biztosan alaposan begyakorlod a terület kiszámítását!
Terület (4. o.)
JÁTÉK! Építsd fel a városodat a mezőre! Számold meg, hány egység a téglalapok, négyzetek és egyéb alakzatok területe, és hasonlítsd össze őket egymással vagy a megadott számmal! Kattints a helyes relációs jelre, és látni fogod a magyarázatot is. Mire az egész város felépül, biztosan alaposan begyakorlod a terület számolását.
22. Területszámítás és integrálás ...
22. Tétel: Területszámítás elemi úton és az integrálszámítás felhasználásával. A tétel kifejtésében a területszámításról fogunk beszélni. Először elemi úton vizsgáljuk meg a témát, síkgeomatriai alakzatok területét részletezzük, majd áttérünk az integrálszámítás felhasználására. A tételt hallani fogod, és látni azt, amit közben érdemes a táblára írnod. Hogyan lehet definiálni egy alakzat területét? A területet úgy értelmezzük, mint egy függvényt, ahol minden síkidomhoz hozzárendelünk egy pozitív számot 3 tulajdonsággal. Ezek a következők: Az egységnégyzet területe 1. Az egybevágó sokszögek területe egyenlő. A 3. tulajdonság pedig úgy szól, hogy ha egy sokszöget feldarabolunk részsokszögekre, akkor a részek területének összege a sokszög területével egyenlő. Hogyan számoljuk ki különböző sokszögek területét? A sokszögek esetén a terület nagyságának meghatározása az egységnyi területtel való összevetés alapján történik. Ezt a szerepet tölti be az egységnégyzet. Nézzük át néhány speciális sokszög területének kiszámítási módját! A téglalap területe két szomszédos oldalának szorzatával egyenlő. A paralelogramma területe az egyik alap és a hozzátartozó magasság szorzata. Részletezzük a háromszög területének képletét, a trapéz területének kiszámítását. Mivel minden sokszög véges számú háromszögre darabolható, ezért a sokszög területe egyenlő a háromszögek területösszegével. A háromszög területének kiszámítására sok képlet van, ezek közül felírtam a leggyakrabban használtakat. Ezekben a képletekben s a félkerület, az r a beírt kör sugara, R pedig a háromszög körülírt körének a sugara. Azt a tételt bizonyítjuk, hogy átalános négyszög területét úgy számíthatjuk ki, hogy az átlók hosszát megszorozzuk a közre zárt szögük szinuszával, és ezt a szorzatot osztjuk kettővel. A bizonyítást a videón részletezzük. Szabályos sokszögek területét úgy kapjuk meg, hogy a középpontjukat összekötjük a csúcsokkal és így n db egyenlő szárú háromszöget kapunk, ezek területe már a középponti szög és a sugár ismeretében kiszámolható. Kör területének kiszámítása. Tétel: Az r sugarú kör területe r2pi-vel egyenlő. Mi a kapcsolat a területszámítás és az integrálszámítás között? A határozott integrállal függvénygörbe vonalával határolt síkidomok területét tudjuk meghatározni. A határozott integrál definíciójához szükségünk van még az intervallum felosztásának a definíciójára. Utána vesszük ennek a felosztásnak egy intervallumát, például az [xi-1;xi] zárt intervallumot. Kis mi legyen az f függvénynek ebben az intervallumban felvett értékeinek alsó határa, nagy Mi pedig a felső határa. Korlátos függvényeknél bizonyítható, hogy ezek az értékek léteznek. Az [xi-1;xi] intervallum fölé téglalapokat szerkesztünk, kettő darabot, kis mi, illetve nagy Mi magassággal. Ha ezt a felosztás összes intervallumában elvégezzük, megkapjuk a vizsgált tartomány egy körülírt és egy beírt sokszögét. Ezeknek a sokszögeknek vizsgáljuk meg a területét. A beírt sokszög területét alsó közelítő összegnek hívjuk, a körülírt sokszög területét pedig felső közelítő összegnek hívjuk. A felosztást finomíthatjuk. Így végtelen sok alsó és felső összeg keletkezik, amelyekről elmondható, hogy semelyik alsó összeg nem lehet nagyobb semelyik felső összegnél. Most már tudjuk definiálni a határozott integrált: Az [a; b] intervallumon korlátos, f függvény integrálható, ha bármely, minden határon túl finomodó felosztássorozatához tartozó alsó és felső összegei sorozatának közös határértéke van. Ezt a közös határértéket nevezzük az f függvény [a; b] intervallumon vett határozott integráljának. Két függvény által közrezárt síkidom területe is kiszámolható a határozott integrállal. Ha f(x)>g(x), akkor az f és g függvények görbéi által közrezárt síkidom területe az f – g függvény integrálásával számolható. A tételt matematika-történeti vonatkozások és gyakorlati alkalmazáshoz kapcsolódó példák zárják. A tétel végén pedig segítünk megtanulni is a tételt, gyakorolhatsz a saját tempódban.
Négyszögek szerkesztése - négyzet, téglalap, rombusz
Speciális négyszögek szerkesztése. Ebben a videóban négyszögek szerkesztését tanuljuk meg. Körzővel és vonalzóval szerkesztjük meg a négyzetet, téglalapot, rombuszt. Az alapos begyakorláshoz ceruzára, papírra, vonalzóra és körzőre is szükséged lesz.
Négyszögek szerkesztése - trapéz, deltoid
Speciális négyszögek szerkesztése - folytatás. Folytatjuk a négyszögek szerkesztését. Körzővel és vonalzóval szerkesztünk rombuszt, szimmetrikus trapézt (húrtrapéz), deltoidot. Az alapos begyakorláshoz ceruzára, papírra, vonalzóra és körzőre is szükséged lesz.