Négyzetgyök
Egy nemnegatív valós a (a ≥ 0) szám négyzetgyöke jelenti azt a nemnegatív számot, aminek a négyzete a. Jele:
(Azaz lefordítva: csak 0, vagy annál nagyobb számból lehet gyököt vonni, és a gyökvonás eredménye is 0, vagy annál nagyobb szám lesz. A gyökvonás a négyzetre-emelés "fordított" művelete: Pl. 4-nek a gyöke 2, mert a 2 az a szám, amit négyztere emelve 4-et kapunk : 22 = 4, emiatt )
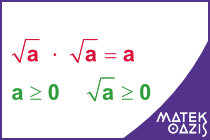
További példák: ;
Feladatok gyökvonással:
1. feladat: Végezzük el a következő műveleteket!
a)
b)
c)
Megoldás:
a)
b)
c)
2. feladat: Egy derékszögű háromszög egyik átfogója a = 5 cm, a másik átfogója b = 12 cm. Milyen hosszú az átfogó?
Megoldás: Felírjuk a Pitagorasz-tétel:
Behelyettesítünk.
Összevonunk.
Mindkét oldalból gyököt vonunk.
A derékszögű háromszög átfogója 13 cm hosszú.
A következő Matek Oázis videókkal tanulhatsz a négyzetgyökről
2006. május, I. rész / 5-12. feladat
A mostani matekvideóban néhány egyszerűbb érettségi feladat megoldását nézzük át. Algebrai tört egyszerűsítése, egy téglatest térfogata, a négyzetgyökvonás finomságai, százalékszámítás, kombinatorika mellett helyet kapott egy kis koordinátageometria, függvényjellemzés és egy halmazos feladat is.
5. Hatványozás, gyökvonás ...
5. tétel : Hatványozás és a hatványfogalom kiterjesztése, a hatványozás azonosságai. Az n-edik gyök fogalma. A négyzetgyök azonosságai. Hatványfüggvények és a négyzetgyökfüggvény. A tétel kifejtésében először a pozitív egész kitevős hatványozásról, a művelet azonosságairól szeretnék beszélni, majd a hatványozás kiterjesztéséről először negatív egészekre, végül a valós számokra. Majd a hatványozás műveletének inverzéről, a gyökvonásról beszélek, a négyzetgyök azonosságairól, hatványfüggvényekről és négyzetgyökfüggvényről, végül ezek jellemző tulajdonságairól. Mi a hatványozás, hogyan értelmezzük pozitív egész számokra? A hatványozás két szám között értelmezett matematikai művelet. Jelölése Amennyiben az a pozitív egész szám, az an pontosan n db azonos, a-val jelölt szám szorzata. n = 1 esetén nem beszélhetünk szorzatról, definíció szerint minden szám első hatványa önmaga. A hatványozás azonosságai. Azonos alapú hatványokat úgy szorzunk össze, hogy az alap változatlan, ezt a kitevők összegére kell emelni. Azonos alapú hatványok hányadosa is velük azonos alapú hatvány lesz, a kitevőt pedig úgy kapjuk, hogy a számláló kitevőjééből kivonjuk a nevező kitevőjét. Ezek az azonosságok könynen igazolhatók a definíció alapján, a videón megmutatjuk, hogyan. A következő azonosság is hasonlóan bizonyítható, hatvány hatványozásakor a kitevők összeszorzódnak. Különböző alapú, de azonos kitevőjű hatványokkal is végezhetünk műveleteket. Ha összeszorozzuk őket, akkor megtehetjük, hogy először az alapokat összeszorozzuk, és csak utána hatványozzuk a szorzatot. Ez egyben azt is jelenti visszafelé, hogy a szorzatot tényezőnként is hatványozhatjuk. Ugyanígy a törtek esetében is a tört hatványa nem más, mint a számláló és a nevező megfelelő hatványának hányadosa. Mit jelent a negatív egész kitevőjű hatvány? A permanencia-elv alapján amennyiben nem a nullát hatványozzuk, bármely szám nulladik hatványát 1-nek definiáljuk. A negatív kitevőt is tudjuk értelmezni, tetszőleges nem nulla valós alap és n pozitív kitevő esetén az lesz. Hogyan értelmezzük, amikor racionális és irracionális szám van a hatvány kitevőjében? Egy a pozitív szám n/m-edik hatványa alatt azt a valós számot értjük, amelyet m. hatványra emelve az a n. hatványát kapjuk. Irracionális kitevőjű hatványt pedig azonos alapú, de racionális kitevős hatványok sorozatának határértékeként fogjuk fel. Igazolhatjuk, hogy az irracionális kitevős hatvány, mint határérték létezik, az azonosságok ugyanúgy érvényben maradnak. A gyökvonás műveletének definíciója. A gyökvonás a megfelelő értelmezési tartomány mellett a hatványozás inverz művelete. Egy nem negatív valós szám 2k-adik, azaz páros gyöke alatt azt a nemnegatív valós számot értjük, amelyet 2k-adik hatványra emelve az a nem negatív valós számot kapjuk vissza. A 2k+1-edik gyök műveletét valós számokon tudjuk végezni, 2k+1-edik gyöke egy valós számnak az a szám lesz, amelyet 2k+1. hatványra emelve az a számot kapjuk vissza. Fontos kapcsolat van a racionális törtkitevő és a gyökvonás között: n-edik gyök ( am) = an/m megfelelő értelmezési tartomány mellett, m pozitív egész szám. Racionális kitevő esetén nem értelmezzük, ha az alap negatív szám, hiszen akkor az m. gyök műveletének elvégzésénél problémák adódhatnának. A négyzetgyök és a köbgyök a két leggyakrabban alkalmazott művelet. A az a nemnegatív valós szám, amelyet önmagával megszorozva az a számot kapjuk vissza. A gyökvonás és a hatványozás művelete felcserélhető, ugyanez a helyzet akkor, ha negatív számról és páratlan gyökről van szó. Viszont ha a valós számok halmazán először emelünk páros kitevőre, majd ugyanennyiedik gyököt is vonunk, akkor a szám abszolútértékét kapjuk meg, nem negatív számok esetén magát a számot, negatív számok esetén pedig az ellentettjüket. A gyökvonás azonosságait ismertetjük. Az a és b nem negatív valós számok. Szorzatuk négyzetgyöke egyenlő a tényezők négyzetgyökének szorzatával. A tétel bizonyítását a videón részletezzük. További azonosságok: a nem negatív és pozitív valós számok estén a hányadosuk négyzetgyöke egyenlő a négyzetgyökeik hányadosával. Nem negatív alap esetén a hatványozás és a négyzetgyökvonás felcserélhető művelet, természetesen a 0 a nulladikon nincs értelmezve. A hatványfüggvényeket, és a tulajdonságaikat nézzük végig. Hatványfüggvénynek nevezzük azt a függvényt, melynek értelmezési tartománya a valós számok halmaza, a függvény x-hez az x n-edik hatványát rendeli hozzá, ahol n tetszőleges pozitív egész szám. Páros n-ek esetén a függvények grafikonja parabola alakú, egyre nagyobb hatvány esetén a parabola egyre szűkebb. Páratlan n-ek esetén pedig egy ilyen szép ívelt görbét kapunk, mivel negatív x-ek esetén a páratlan hatvány negatív lesz. A függvények jellemzésére is kitérünk, értékkészlet, páros/páratlan tulajdonság, monotonitás, szélsőérték, korlátosság, folytonosság, differenciálhatóság, integrálhatóság szempontjai alapján. Megnézzük azt is, hogyan változnak transzformált függvények esetén a függvény tulajdonságai. Mit kell tudni a négyzetgyökfüggvényről és tulajdonságairól? A négyzetgyökfüggvény a nemnegatív valós számok halmazáról képez le valós számokhalmazára, x-hez annak négyzetgyökét rendeli. Grafikonja egy fél fektetett parabola. A nemnegatív számok halmazán ez a függvény az függvény inverze. Értelmelmezési tartománya és értékkészlete a nemnegatív valós számok halmaza. További szempontok a függvényjellemzéshez: monotonitás, szélsőérték, korlátosság, folytonosság, differenciálhatóság, integrálhatóság. A hatványozás és a gyökvonás rengeteg helyen kap szerepet a feladatok megoldásában. Egyenletekben, geometriában, térgeometriában, Hasonlósági feladatok, egyéb geometriai számítások esetén gyakran kell hatványozni vagy gyököt vonni. Ugyanakkor a kamatos kamat számításnál, mértani sorozatoknál, számrendszerek, vagy akár a mértékváltás esetén is fontos.
Négyzetgyökfüggvény, törtfüggvény
Ez a videó további függvényekkel kapcsolatos ismeretek gyakorlására szolgál. Négyzetgyök-függvény, törtfüggvény. A függvények jellemzését gyakorolhatod ezekkel a feladatokkal. Értelmezési tartomány és értékkészlet, zérushely, növekedés-fogyás (csökkenés), valamint a szélsőértékek (minimum és maximum), sőt: páros és páratlan függvény. Mindegyikkel tisztában vagy, mit jelent?
Négyzetgyökös egyenletek, emelt szint
TESZT! Tedd próbára tudásod a feladatokkal, melyekkel gyakorolhatod az emlet szintű négyzetgyökös egyenletek megoldását. Hány megoldása van az egyenletnek? Mi a megoldása az egyenletnek? Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.















