Mértani sorozat
Az an sorozat mértani sorozat, ha van olyan a és q szám, hogy a1 = a és an+1 = an · q.
Ebben a definícióban n azt jelenti, hogy a sorozat hányadik tagjáról van szó (a1 a sorozat első tagja), q a sorozat "hányadosa", idegen szóval kvóciense.
q megmutatja, hogy a sorozat bármelyik tagja hányszorosa az előző tagnak. (Azért nevezzük hányadosnak a q-t, mert ha a 2. tagot osztjuk az elsővel, ennyi lesz a hányados. Ugyanúgy, ha az n+1. tagot osztjuk az n. taggal, szintén q-t kapunk. )
Ha ismerjük a sorozat első tagját és a kvócienst, akkor a sorozat bármelyik tagját meg tudjuk határozni: an = a1 · qn-1.
Ha tudjuk az első tagot és a hányadost, akkor a sorozat első n tagjának az összegét is ki tujduk számolni ezzel a képlettel: (ha q ≠ 1)
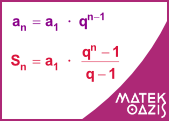
Példa mértani sorozattal
Feladat: Az an mértani sorozatban a3 = 45 és a4 = 135. Határozzuk meg a sorozat első tagját és a kvóciensét! Adjuk meg a sorozat első 10 tagjának az összegét!
Megoldás: Mivel an+1 = an · q, ezért ebbe behelyettesítve:
a4 = a3 · q
135 = 45q
3 = q
Az első tag meghatározásához használjuk a an = a1 · qn-1 képletet.
a3 = a1 · q3-1
45 = a1 · 32
5 = a1.
Az első 10 tag összegéhez behelyettesítünk az első n tag összegére vonatkozó képletbe.
Tehát a sorozat első tagja 5, hányadosa 3, első 10 tagjának összege pedig: 147 620.
A következő Matek Oázis videókkal tanulhatsz a mértani sorozatokról
2007. május / I. - 1-12. feladat
A mostani matekvideóban ismét egy matekérettségi feladatsor megoldásait nézzük végig, pontosabban egy feladatsor I.részének, tehát 12 alapfeladatnak a részletes kidolgozását. A feladatsor egy tört egyszerűsítésével kezdődött, aztán egy mértani sorozatos példa jött, majd a háromszög-egyenlőtlenséggel kapcsolatban 2 állítás. Egy egyszerű szöveges példát is tettek a feladatok közé. Három(!) függvényes feladat volt a 12 példa között: egy másodfokú függvény szélsőértékét kellett meghatározni, egy grafikonjával adott függvénynél megadni, hogy hol nő illetve hol csökken a függvény, majd egy függvényértékből kellett visszaszámolni, hogy azt az értéket milyen x-nél veszi fel a függvény (vagyis tulajdonképpen egy egyenletet kellett megoldani). Volt még szinusz-tétel, módusz és medián-számítás, logaritmus és valószínűségszámítás is.
2006. február / I. - 1-12. feladat
Ebben a matek tananyagban a 2006. februári matek érettségi feladatsor első 12 feladatának megoldásait nézzük át részletesen. Mértani sorozat, a hatványozás azonosságai, logaritmus-azonosságok, kombinatorika, valószínűség, algebra, gráfok, vektorok, százalékszámítás és halmazok -ezek a témakörök mind előkerültek a feladatokban.
2007. október, II. rész / 16-18. feladat
Ez a videó három összetett matekérettségi feladat megoldását mutatja be részletesen a 2007-es októberi érettségi feladatsorból. Az első feladat egy jó bonyolult szöveges feladat volt, némi százalékszámítással és valószínűségszámítással. Sőt, még egy másodfokú egyenlőtlenséget is meg kellett oldani közben. A 17. példában egy kombinatorikai és egy valószínűségszámítási kérdés után egy mértani sorozatra vezető kérdés következett. Az utolsó példa sem volt könnyebb az előzőknél: egy kúpról, a kiterített palástjáról és a bele írt gömbről kellett kiszámolni adatokat.
2009. okt.: I. rész 1-12. feladat
Matematika októberi érettségi feladatsor I. rész12 feladata megoldásokkal: Számtani,mértani közép; Halmazos; Valószínűségszámítás; Exponenciális egyenlet; Szögfüggvény alkalmazása derékszögű háromszögben; Mértani sorozat; Függvény hozzárendelési szabálya; Logaritmusos egyenlet; Térgeometria; Trigonometria feladat
Mértani sorozatok, kamatos kamat
TESZT! Feladatok mértani sorozat és kamatos kamat számítás gyakorlásához. Számold ki a mértani sorozat n-edik elemét, az első n tag összegét, vagy ha ezek meg vannak adva, akkor abból megkaphatod az első elemet és a hányadost. Ha bankba teszed a pénzedet mennyit kapsz vissza néhány év múlva?
5. Hatványozás, gyökvonás ...
5. tétel : Hatványozás és a hatványfogalom kiterjesztése, a hatványozás azonosságai. Az n-edik gyök fogalma. A négyzetgyök azonosságai. Hatványfüggvények és a négyzetgyökfüggvény. A tétel kifejtésében először a pozitív egész kitevős hatványozásról, a művelet azonosságairól szeretnék beszélni, majd a hatványozás kiterjesztéséről először negatív egészekre, végül a valós számokra. Majd a hatványozás műveletének inverzéről, a gyökvonásról beszélek, a négyzetgyök azonosságairól, hatványfüggvényekről és négyzetgyökfüggvényről, végül ezek jellemző tulajdonságairól. Mi a hatványozás, hogyan értelmezzük pozitív egész számokra? A hatványozás két szám között értelmezett matematikai művelet. Jelölése Amennyiben az a pozitív egész szám, az an pontosan n db azonos, a-val jelölt szám szorzata. n = 1 esetén nem beszélhetünk szorzatról, definíció szerint minden szám első hatványa önmaga. A hatványozás azonosságai. Azonos alapú hatványokat úgy szorzunk össze, hogy az alap változatlan, ezt a kitevők összegére kell emelni. Azonos alapú hatványok hányadosa is velük azonos alapú hatvány lesz, a kitevőt pedig úgy kapjuk, hogy a számláló kitevőjééből kivonjuk a nevező kitevőjét. Ezek az azonosságok könynen igazolhatók a definíció alapján, a videón megmutatjuk, hogyan. A következő azonosság is hasonlóan bizonyítható, hatvány hatványozásakor a kitevők összeszorzódnak. Különböző alapú, de azonos kitevőjű hatványokkal is végezhetünk műveleteket. Ha összeszorozzuk őket, akkor megtehetjük, hogy először az alapokat összeszorozzuk, és csak utána hatványozzuk a szorzatot. Ez egyben azt is jelenti visszafelé, hogy a szorzatot tényezőnként is hatványozhatjuk. Ugyanígy a törtek esetében is a tört hatványa nem más, mint a számláló és a nevező megfelelő hatványának hányadosa. Mit jelent a negatív egész kitevőjű hatvány? A permanencia-elv alapján amennyiben nem a nullát hatványozzuk, bármely szám nulladik hatványát 1-nek definiáljuk. A negatív kitevőt is tudjuk értelmezni, tetszőleges nem nulla valós alap és n pozitív kitevő esetén az lesz. Hogyan értelmezzük, amikor racionális és irracionális szám van a hatvány kitevőjében? Egy a pozitív szám n/m-edik hatványa alatt azt a valós számot értjük, amelyet m. hatványra emelve az a n. hatványát kapjuk. Irracionális kitevőjű hatványt pedig azonos alapú, de racionális kitevős hatványok sorozatának határértékeként fogjuk fel. Igazolhatjuk, hogy az irracionális kitevős hatvány, mint határérték létezik, az azonosságok ugyanúgy érvényben maradnak. A gyökvonás műveletének definíciója. A gyökvonás a megfelelő értelmezési tartomány mellett a hatványozás inverz művelete. Egy nem negatív valós szám 2k-adik, azaz páros gyöke alatt azt a nemnegatív valós számot értjük, amelyet 2k-adik hatványra emelve az a nem negatív valós számot kapjuk vissza. A 2k+1-edik gyök műveletét valós számokon tudjuk végezni, 2k+1-edik gyöke egy valós számnak az a szám lesz, amelyet 2k+1. hatványra emelve az a számot kapjuk vissza. Fontos kapcsolat van a racionális törtkitevő és a gyökvonás között: n-edik gyök ( am) = an/m megfelelő értelmezési tartomány mellett, m pozitív egész szám. Racionális kitevő esetén nem értelmezzük, ha az alap negatív szám, hiszen akkor az m. gyök műveletének elvégzésénél problémák adódhatnának. A négyzetgyök és a köbgyök a két leggyakrabban alkalmazott művelet. A az a nemnegatív valós szám, amelyet önmagával megszorozva az a számot kapjuk vissza. A gyökvonás és a hatványozás művelete felcserélhető, ugyanez a helyzet akkor, ha negatív számról és páratlan gyökről van szó. Viszont ha a valós számok halmazán először emelünk páros kitevőre, majd ugyanennyiedik gyököt is vonunk, akkor a szám abszolútértékét kapjuk meg, nem negatív számok esetén magát a számot, negatív számok esetén pedig az ellentettjüket. A gyökvonás azonosságait ismertetjük. Az a és b nem negatív valós számok. Szorzatuk négyzetgyöke egyenlő a tényezők négyzetgyökének szorzatával. A tétel bizonyítását a videón részletezzük. További azonosságok: a nem negatív és pozitív valós számok estén a hányadosuk négyzetgyöke egyenlő a négyzetgyökeik hányadosával. Nem negatív alap esetén a hatványozás és a négyzetgyökvonás felcserélhető művelet, természetesen a 0 a nulladikon nincs értelmezve. A hatványfüggvényeket, és a tulajdonságaikat nézzük végig. Hatványfüggvénynek nevezzük azt a függvényt, melynek értelmezési tartománya a valós számok halmaza, a függvény x-hez az x n-edik hatványát rendeli hozzá, ahol n tetszőleges pozitív egész szám. Páros n-ek esetén a függvények grafikonja parabola alakú, egyre nagyobb hatvány esetén a parabola egyre szűkebb. Páratlan n-ek esetén pedig egy ilyen szép ívelt görbét kapunk, mivel negatív x-ek esetén a páratlan hatvány negatív lesz. A függvények jellemzésére is kitérünk, értékkészlet, páros/páratlan tulajdonság, monotonitás, szélsőérték, korlátosság, folytonosság, differenciálhatóság, integrálhatóság szempontjai alapján. Megnézzük azt is, hogyan változnak transzformált függvények esetén a függvény tulajdonságai. Mit kell tudni a négyzetgyökfüggvényről és tulajdonságairól? A négyzetgyökfüggvény a nemnegatív valós számok halmazáról képez le valós számokhalmazára, x-hez annak négyzetgyökét rendeli. Grafikonja egy fél fektetett parabola. A nemnegatív számok halmazán ez a függvény az függvény inverze. Értelmelmezési tartománya és értékkészlete a nemnegatív valós számok halmaza. További szempontok a függvényjellemzéshez: monotonitás, szélsőérték, korlátosság, folytonosság, differenciálhatóság, integrálhatóság. A hatványozás és a gyökvonás rengeteg helyen kap szerepet a feladatok megoldásában. Egyenletekben, geometriában, térgeometriában, Hasonlósági feladatok, egyéb geometriai számítások esetén gyakran kell hatványozni vagy gyököt vonni. Ugyanakkor a kamatos kamat számításnál, mértani sorozatoknál, számrendszerek, vagy akár a mértékváltás esetén is fontos.
10. Mértani sorozat ...
10. tétel: Mértani sorozat, az első n tag összege, végtelen mértani sor. Kamatszámítás, gyűjtőjáradék, törlesztőrészlet. Exponenciális folyamatok a társadalomban és a természetben. Egy kész szóbeli feleletet fogsz hallani, és látni fogod, amit érdemes neked is felírnod a táblára a vizsgán. Az anyag második felében pedig segítünk mindezt megtanulni. Milyen sorozat a mértani sorozat, és hogyan kell kiszámolni az első n tag összegét? Azokat a számsorozatokat, amelyekben az egymást követő tagok hányadosa állandó, mértani sorozatnak nevezzük. Ez az állandó a mértani sorozat hányadosa, amit idegen szóval kvóciensnek mondunk. Ez a definíció kizárja azt, hogy a sorozat bármely tagja, illetve kvóciense 0 legyen. Ha mértani sorozat első tagja a1, hányadosa q, akkor az n. tagot úgy számolhatjuk, hogy az első tagot megszorozzuk a kvóciens n-1. hatványával. Azt a tételt bizonyítjuk a videón, amelyik a mértani sorozat első n tagjának összegére vonatkozik. A mértani sorozat fogalmát már az ókori egyiptomiak is ismerték, és összegük is érdekelte őket. Konkrét feladatok esetén ki is tudták számolni az összeget, erről tanúskodik Rhind-papirusz ami i. e. 1750 körül íródott. Mi a különbség a mértani sor és a mértani sorozat között? A mértani sor egy végtelen összeg. A szumma i megy 1-től végtelenig a1 szer qi-1 -en úgynevezett végtelen összeget végtelen mértani sornak nevezzük. Ha ennek a végtelen összegnek létezik határértéke, és az véges, akkor azt a végtelen mértani sor összegének nevezzük, és S-sel jelöljük. Tétel mondja ki, hogy ha a a mértani sorozat első tagja a1, és hányadosa abszolútértéke kisebb, mint 1, akkor az összege úgy számolható, hogy a1/(1-q). A végtelen mértani sor összegképletének felhasználásával tudjuk például a végtelen szakaszos tizedes törteket két egész szám hányadosaként felírni A kamatszámítás kapcsolatban van a mértani sorozatokkal. Ha egy pénzösszeget, azaz betétet egy bankban elhelyezünk, akkor a bank a pénzünk használatáért a betétünkre bizonyos kamatot ad. A kamat és a betét százalékban kifejezett hányadosát kamatlábnak nevezzük. Hasonlóan, ha a bank pénzét használjuk, akkor ezért a felvett hitelért bizonyos ellenszolgáltatást kell nyújtanunk. Matematika feladatokban azzal a feltevéssel élünk, hogy a futamidő alatt a kamatláb mértéke állandó. Egyszerű kamatozás során a kiinduló összeg, azaz az alaptőke bizonyos százalékban kifejezett hányadát szabályos időközönként hozzáadják a tőkéhez. Ezt a százalékot kamatlábnak nevezzük. De számolhatunk kamattényezővel, q-val is, ami a kamatláb 100-ad részével tér el az 1-től: értéknövekedés esetén q=1+p/100, értékcsökkenés esetén q=1-p/100. Kamatos kamatról akkor beszélünk, ha a kamatozási időszak végén a kamatot hozzáadják a tőkéhez, és utána ez a megnövekedett érték kamatozik. A kamatos kamat számítása a mértani sorozat alkalmazásának olyan speciális esete, amikor a sorozatnak van nulladik tagja, amit a pénzügyi számításokban A-val jelölünk. Ha egy A összeg p%-kal kamatozik évente, akkor az n-edik év végére kiszámolható, hogy menyni az értéke. Ha ezt a kamattényezővel fejezzük ki, amit q-val jelöljük, ekkor az An=A*qn -nel. Ez egy olyan mértani sorozat n. eleme, amelynek első eleme Aq, hányadosa pedig q. Az An összefüggésében négy mennyiség szerepel, közülük bármely hármat ismerve a negyedik kiszámolható. Mi a gyűjtőjáradék, és hogyan lehet kiszámolni? Gyűjtőjáradékról akkor beszélünk, ha egy alapösszeget egyenlő időközönként ugyanakkora összeggel növelünk, vagyis egyenlő időközönként azonos összeget elhelyezünk a bankban ugyanazon a számlán. Gyűjtjük a pénzt, és minden betett összegünk kamatos kamattal kamatozik. A gyűjtőjáradék számítása úgy zajlik, hogy minden év elején egy a összeget teszünk a bankba, és ez p%-kal kamatozik évente úgy, hogy a következő év elején a megnövekedett összeghez tesszük hozzá az újabbat. Ha a kamattényező q=1+p/100, akkor az n. év végén a vagyonunk egy olyan mértani sorozat elsőn n elemének az összege, ahol a1=aq. Ezt felhasználva n. év végére a gyűjtött vagyonunk kiszámolható. Hogyan kell törlesztőrészletet számolni? Egy mindennapokban gyakran használt fogalommal folytatnám a feleletet. Törlesztőrészletről akkor beszélünk, ha egy hitelt egyenlő időközönként ugyanakkora összeggel fizetünk vissza, azaz egyenlő időközönként azonos összeggel csökkentjük a tartozásunkat, vagyis törlesztjük a hitelt, minden befizetett összeg után csak a fennálló tartozásra fizetünk kamatos kamatot. Hogyan kell törlesztőrészletet számítani? Felveszünk n évre Sn nagyságú hitelt évi p%-os kamatra, és minden évben „a” összeget törlesztünk. A törlesztés mindig az év végén történik, a kamatszámítás után, minden évben azonos a összegekkel. A tartozásunkra így felírható a képlet. A felvett Sn-hitel kamatozik a kamattényezővel, majd ebből levonunk a-t, hiszen azt törlesztjük az adott évben. A zárójelek közepébe írtam, hogy a felvett hitel kamatozik, ezt jelenti az Sn*q. Ebből törlesztünk, azaz levonunk a tartozásunkból a-t. Ezután ez kamatozik és ebből vonunk le megint a-t. Az utolsó év végén a fennálló tartozásunk kamatozik még egyet, ekkor a tartozásunk éppen a lesz, amit törlesztünk is. Ezután a fennálló tartozásunk 0 forint lesz. (… (((Snq-a) q-a)q-a)) q-a=0 Ebből az összefüggésből az a törlesztőrészlet meghatározható. A tételben kifejtésében még beszélünk az exponenciális folyamatokról a társadalomban és a természetben.























