Logaritmus azonosságok
A b szám a alapú logaritmusa az a kitevő, amelyre a-t emelve b-t kapunk, ahol a > 0; a ≠ 1 és b > 0. Jele: loga b.
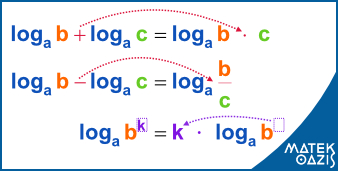
A logaritmus alapja mindig pozitív szám és nem 1. A logaritmus argumentumába (hasába) csak pozitív szám szerepelhet!
Példák a logaritmus azonosságok használatáról
Feladat: Számítsuk ki x értékét, ha
Megoldás: Az a) feladatban felhasználjuk azt az azonosságot, hogy
A logaritmusfüggvény szigorú monotonitása miatt elhagyható a logaritmus
A b) feladatban két azonosságot használjuk fel. Előszört azt, hogy . Ezután azt használjuk fel, hogy

A következő Matek Oázis videókkal tanulhatsz a logaritmus azonosságairól
Hatványozás (ismétlés)
A hatványozás, a gyökvonás és a logaritmus összefüggenek egymással. A hatványozás az alapja mindennek, tehát nagyon fontos, hogy tisztában legyél ezek azonosságaival, és alkalmazni is tudd őket. Átismételjük a hatványozást egész kitevővel. Meghatározzuk a hatványozás definícióját, a hatványozás azonosságait. Feladatokat oldunk meg együtt a hatványozás gyakorlására.
Logaritmus felmérő
TESZT! Az alábbi tesztben próbára teheted tudásod a logaritmus definíció és logaritmus azonosságok alkalmazása, logaritmikus egyenletek, egyenlőtlenségek, egyenlet-rendszerek és a logaritmus függvény ábrázolása terén. Dolgozz önállóan, majd a kiértékelésben levezetjük a megoldást lépésről lépésre.
2006. február / I. - 1-12. feladat
Ebben a matek tananyagban a 2006. februári matek érettségi feladatsor első 12 feladatának megoldásait nézzük át részletesen. Mértani sorozat, a hatványozás azonosságai, logaritmus-azonosságok, kombinatorika, valószínűség, algebra, gráfok, vektorok, százalékszámítás és halmazok -ezek a témakörök mind előkerültek a feladatokban.
6. A logaritmus ...
6. tétel: A logaritmus fogalma és azonosságai. Az exponenciális és a logaritmusfüggvény. Az inverzfüggvény. A logaritmus fogalmát definiáljuk, majd a logaritmus műveletének azonosságairól, az exponenciális a és a logaritmusfüggvényről fogunk beszélni, végül a függvények inverzéről, azok képzéséről. A logaritmus definíciója, tulajdonságai. logab az a valós szám, amelyre az a-t emelve b -t kapjuk. a,b > 0, és a nem 1 (Részletesen indokoljuk, hogy miért kellenek ezek a kikötések) Másképpen úgy is mondhatjuk, hogy az logab = c és az ac = b ekvivalens állítások. A 10-es alapú logaritmust lg-vel, a természetes, vagyis e alapú logaritmust ln-nel jelöljük. Melyek a logaritmus azonosságai? A logaritmus műveletének azonosságai közül az első a szorzat logaritmusára vonatkozik: Szorzat logaritmusa a tényezők logaritmusának összege, visszafelé úgy is mondhatjuk, hogy azonos alapú logaritmusokat úgy adunk össze, hogy az argumendumokat összeszorozzuk. A tételt bizonyítjuk is a videón. További logaritmus azonosságok:. Hányados logaritmusa a számláló és a nevező logaritmusának különbsége. Ha pedig egy hatványnak vesszük a logaritmusát, akkor az nem más, mint az alap logaritmusának és a kitevőnek a szorzata. Ilyenkor a kitevőt, mint szorzótényezőt a logaritmus elé írjuk. Egy logaritmusos kifejezést más alapra is átírhatunk, az ismert összefüggés alapján. Ezt az azonosságot is bebizonyítjuk. Mit kell elmondani az exponenciális függvényekről? Exponenciális függvénynek nevezzük azt a valós számok halmazáról leképező függvényt, amely az x-hez az ax -et rendeli, ahol az a egy pozitív valós szám. Ha a függvény grafikonját szeretnénk megrajzolni, akkor két esetet kell megkülönböztetnünk az alaptól függően: Ha az alap 0 és 1 közötti, akkor az ax grafikonja szigorúan monoton csökken, ha pedig 1-nél nagyobb, akkor szigorúan monoton nő. Amennyiben az alap 1, a konstans 1 függvényről van szó. Mindkét esetben az értelmezési tartomány a valós számok halmaza, az értékkészlet pedig a pozitív valós számok halmaza. Közös tulajdonsága az ax típusú exponenciális függvényeknek, hogy grafikonjuk áthalad a ( 0; 1) ponton, hiszen bármely pozitív szám nulladik hatványa 1. Szélsőértékük nincs, felülről nem korlátosak, tehát nem korlátosak. Konvex függvények, zérushelyük nincs. Nem párosak és nem is páratlanok. Ezek a függvények a folytonosság miatt differenciálhatók és integrálhatók is. A logaritmus függvényeknek mi a közük az exponenciális függvényekhez? A logaritmus függvény a megfelelő exponenciális függvény inverze, a pozitív valós számok halmazáról képez le a valós számok halmazára, x-hez annak a alapú logaritmusát rendeli. Ha a logaritmus alapja 1-nél nagyobb szám, akkor a függvény szigorúan monoton nő, ha 0 és 1 közötti szám, akkor szigorúan monoton csökken. Negatív alapot és 1-es alapot nem értelmezünk logaritmus esetén. Értelmezési tartomány a pozitív számok halmaza, értékkészlete a valós számok halmaza. Zérushelyük van x=1-nél. Szélsőértékük nincs, sem alulról, sem felülről nem korlátosak. Ha az alap 1-nél nagyobb, a függvény konkáv, ha 0 és 1 közötti, akkor konvex. Nem párosak és nem is páratlanok. A függvények a folytonosság miatt differenciálhatók és integrálhatók is. Mit jelent az inverz függvény? Az f függvény inverze az f -1 ha az f értelmezési tartományának minden x elemére igaz, hogy f(x) eleme a f -1 értelmezési tartományának és f -1 (f(x)) = x. Ha az f és az f -1 függvények egymásnak inverzei, akkor az f értelmezési tartománya az f -1 értékkészlete, az f értékkészlete azf -1 értelmezési tartománya. Az f és az f -1 akkor grafikonjai tengelyesen tükrösek az y = x egyenletű egyenesre nézve. Megnézünk néhány példát az inverz függvényre a videón. Például inverze egymásnak a négyzetgyök függvény és az x2 függvény a megfelelő értelmezési tartomány mellett, vagy az f(x) = 3x és az 1/3 x is. Algebrai úton általában könnyen megkaphatjuk egy függvény inverzének hozzárendelési szabályát. Kitérünk még arra is, hogy az exponenciális és logaritmusos kifejezésekkel hol találkozhatunk, illetve az exponenciális, logaritmusos egyenletek megoldása milyen hétköznapi, v. műszaki problémák megoldásánál fontos. Említünk matematikatörténeti vonatkozásokat is.