Ismétléses variáció
Amikor n darab különböző elemből kell feltöltenünk k különböző helyet úgy, hogy egy elemet többször is választhatunk, akkor ismétléses variációról beszélünk.
Mivel mind a k helyre n-féleképpen választhatunk ilyenkor az elemek közül, összesen nk- féleképpen tölthetjük fel a k helyet. (Ennyi tehát n elem k-ad osztályú ismétléses variációinak a száma)
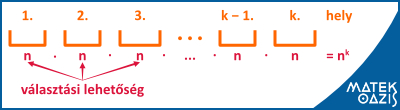
Példa az ismétléses variáció megértéséhez
Feladat: Az 1; 2; 3; 4; 5 számok felhasználásával hány négyjegyű számot készíthetnük, ha egy számjegyet többször is felhasználhatunk?
Megoldás: Ebben a feladatban n = 5, mert öt szám közül kell választanunk, és k = 4, hiszen ennyi helyre kell variálni a számokat.
Az első helyre választhatjuk az öt szám bármelyikét. A másodikra, harmadikra és negyedikre is.
A kiválasztások egymástól függetlenek (például, ha az első helyre 4-est választottunk, akkor az nem befolyásolja, hogy a második helyre mit választunk), ezért a lehetőségek számát összeszorozzuk.
Így a lehetőségek száma 5 · 5 · 5 · 5 = 54.

