Ismétlés nélküli variáció
Amikor n darab különböző elem közül kiválasztunk k darabot úgy, hogy a kiválasztás sorrendje is számít, akkor ezt az n elem k-ad osztályú ismétlés nélküli variációjának nevezzük.
Ezek lehetséges száma: . Azaz n különböző elem közül k darabot a sorrend figyelembevételével
-féleképp választhatunk ki.
Ezt úgy is megkaphatjuk, ha végiggondoljuk, hogy az 1. helyre n elem közül válaszhtaunk, a másodikra már csak n - 1 közül, a harmadikra n - 2 közül, stb... a k. helyre (n - k + 1)-féleképpen. Ezeket össze kell szorozni, így: n · (n - 1) · (n - 2) ·... · (n - k + 1) lehetőséget kapunk.
És n · (n - 1) · (n - 2) ·... · (n - k + 1) =
Példa az ismétlés néküli variáció megértéséhez
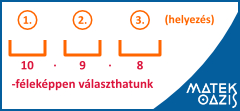
Feladat: Egy futóversenyen 10-en indulnak. Hányféleképp alakulhatnak a dobogós helyezések?
Megoldás: A dobogón három hely van. A 10 emberből 3-at kell kiválasztani, aki dobogóra áll. Azonban nekik számít a sorrendjük, hiszen neked se lenne mindegy, hogy a dobogó melyik fokára állsz.
Az ismétlés nélküli variáció képletét kell használnunk. Eszerint:
Másféleképpen: . Az első helyre 10 ember közül választhatok, a másodikra már csak 9-ből (hisz aki az 1. helyezett lett, ő már nem lehet 2. is) , a harmadik helyre 8-ból. Bármelyikük került az 1. helyre, ahhoz 9-féleképpen választhatunk 2.-at, ami 10 · 9 lehetőség az első 2 hely betöltésére. És mivel mindegyiket folytathatjuk 8-féleképpen, ezért összesen: 10 · 9 · 8 = 720 lehetőséget kapunk.
(Ez úgy jön ki, ha a törtet egyszerűsítjük 7!-sal.)
A következő Matek Oázis videókkal tanulhatsz az ismétlés nélküli variációról
24. Permutációk, variációk...
24. tétel: Permutációk, variációk. A binomiális eloszlás. A valószínűség kiszámításának geometriai modellje. A kidolgozott tételt látod-hallod a videón, pontosabban azt látod, amit a vizsgán érdemes felírnod a táblára. Az előző tételhez hasonlóan itt is kombinatorikai és valószínűségszámítási ismereteket kell bemutatni. Mi az a permutáció, milyen feladatokhoz kapcsolódik, hogyan kell kiszámolni? Mi a különbség az ismétlés nélküli és az ismétléses permutáció között? Egy adott n elemű halmaz elemeinek egy ismétlés nélküli permutációján az n különböző elem egy sorba rendezését, azaz sorrendjét értjük. Tétel: Egy n elemű halmaz ismétlés nélküli permutációinak száma n faktoriálissal egyenlő. Bizonyítás: Az n db hely közül az első helyre n féle elem közül választhatok, ezért a lehetőségek száma n. A második helyre már csak (n-1) elem közül tudok választani, hiszen az első helyre már választottam. Ezt a gondolatmenetet folytatva egyértelmű, hogy az utolsó előtti helyre 2, az utolsó helyre pedig 1-féle elem közül tudok választani. A választások egymástól függetlenek, így a lehetőségek számát össze kell szorozni, így kapunk n!-t. Ha az n elem között van n1, n2, …, nk egymással megegyező, akkor az elemek egy sorba rendezését ismétléses permutációnak nevezzük. Ha n elem között n1, n2, … nk db megegyező van, és n1+n2+…+ nk=n, akkor az ismétléses permutációk számához n!-t osztani kell n1! -sal, n2!-sal, stb… nk!-sal. Mi a variáció, mi a különbség az ismétlés nélküli és az ismétléses variáció között? Hogyan kell kiszámolni a lehetséges variációk számát? Vegyünk n db egymástól különböző elemet. Ha ezekből kiválasztunk k db-ot minden lehetséges módon úgy, hogy a kiválasztott elemek sorrendje is számít, akkor az n elem k-ad osztályú ismétlés nélküli variációját kapjuk. Kikötjük, hogy k kisebb vagy egyenlő, mint n. Azt a tételt bizonyítjuk a videón, hogy az n elem k-ad osztályú ismétlés nélküli variációinak száma n!/(n-k)! Definiáljuk az ismétléses variációt: Legyen n db egymástól különböző elemünk. Ha ezekből kiválasztunk k db-ot az összes lehetséges módon úgy, hogy a kiválasztott elemek sorrendje is számít, és egy elemet többször is választhatunk, akkor az n elem egy k-ad osztályú ismétléses variációját kapjuk. Tétel mondja ki, hogy n elem k-ad osztályú ismétléses variációinak száma nk. Mit jelent a valószínűségi változó? Ehhez először szükséges definiálni a valószínűségi változót. A diszkrét valószínűségi változó az eseménytéren értelmezett valós értékű függvény. Általában kszível, vagy nagy X-szel jelöljük. Ha a valószínűségi változó lehetséges értékeinek száma véges, vagy megszámlálhatóan végtelen, akkor diszkrét valószínűségi változóról beszélünk. Milyen eloszlás a binomiális-eloszlás? A binomiális-eloszlás olyan kísérletnél fordul elő, amelynek csak két kimenetele lehetséges, azaz A esemény vagy bekövetkezik vagy nem. Azt is mondhatjuk, hogy A esemény bekövetkezése a kedvező eset, ennek a valószínűsége p. A kedvezőtlen esemény valószínűsége, azaz, hogy A esemény nem következik be 1-p. Tétel: Binomiális eloszlásnál, ha a kísérletet n-szer ismételjük, akkor annak a valószínűsége, hogy az A esemény k-szor következik be, úgy adható meg, hogy n alatt a k-szor pk*(1-p)n-k. Itt is ki kell kötni, hogy k kisebb vagy egyenlő, mint n. Megemlíteném, hogy binomiális eloszlásra vezetnek a visszatevéses mintavétel esetei. A binomiális-eloszlás várható értéke könnyen számolható. Az eloszlás két paraméterét n-t és p-t kell összeszorozni. Matematikatörténeti vonatkozásokat is említünk a valószínűségszámítással és kombinatorikával kapcsolatban. Mi a geometriai valószínűség? Hogyan kell kiszámítani? Ha az eseménytér nem megszámlálható halmaz, de mérhető (például van hossza, területe vagy térfogata), az eseményei mérhetők, és valószínűségük egyenesen arányos a méretükkel, akkor ezt az eseményteret geometriai valószínűségi mezőnek nevezzük. Ekkor az A esemény valószínűsége számítható úgy, hogy az A eseménynek megfelelő részalakzat mértékét elosztjuk a kísérlettel kapcsolatos teljes alakzat mértékével. Ezt általában úgy jelöljük, hogy m/M. Néhány gyakorlati példát sorolunk fel végül a geometriai valószínűség alkalmazására.


