Háromszögbe írható kör

Minden háromszögbe tudunk kört rajzolni.

A beírt kör középpontja a háromszög szögfelező egyeneseinek a metszéspontja. 

A beírt kör a háromszög minden oldalát egy-egy pontban érinti.

Példa a háromszögbe írható körről

Feladat: Szerkesszük meg az ABC háromszög beírt körét, ha a = 6 cm b = 9 cm és az a és b oldalak bezárt szöge 𝛾 = 60°.

Megoldás: Megszerkesztjük a háromszöget. Könnyű dolgunk van: megszerkesztjük a 60°-ot körző segítségével, és egyik szögszárára felmérünk 6 cm-t, a másikra pedig 9 cm-t. Ezeket a metszéspontokat összekötve meg is kaptuk a háromszöget.

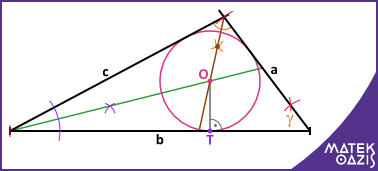
Ezután szerkesztünk két szögfelezőt (zöld és barna egyenesek), ezek metszéspontja adja meg a beírt kör O középpontját.

A metszéspontból merőlegest bocsátunk b oldalra (szürke szakasz)T pont.

A körzőnket O-ba bökjük, kinyitjuk OT hosszúságúra, és berajzoljuk a körvonalat. ezzel kész is a háromszögbe írt kör.