Deltoid
A deltoid olyan négyszög, aminek két-két szomszédos oldala egyenlő hosszú. (Ilyen a papírsárkány formája is.)
Másképp: a deltoid olyan tengelyesen szimmetrikus négyszög, aminek az egyik átlója a tükörtengelye.
Megkülönböztetünk konvex (1) és konkáv (2) deltoidot.
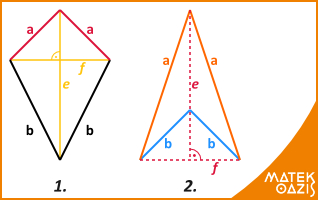
A deltoid átlói merőlegesek egymásra.
A deltoid rombusz, ha mind a négy oldala ugyanolyan hosszú.
A deltoid területe: , ahol e és f az átlók hossza.
Példák deltoiddal
1. feladat: Döntsük el, hogy az alábbi állítások közül melyikk igaz, melyik hamis!
a) Minden négyzet deltoid.
b) Minden deltoid négyzet.
c) Minden paralelogramma deltoid.
Megoldás:
a) Az állítás igaz. Minden négyzetnek két-két szomszédos oldala egyenlő hosszú, és még mind a két átlója is tükörtengely.
b) Az állítás hamis. Az ábrán lévő (1) és (2) deltoidok egyértelműen nem négyzetek.
c) Az állítás hamis. Például ennek a paralelogrammának nincsenek azonos hosszúságú szomszédos oldalai:
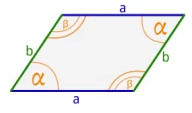
2. feladat: Egy deltoid átlói e = 6 cm és f = 11 cm. Mekkora a deltoid területe?
Megoldás: Minden adatot ismerünk, behelyettesítünk a területképletbe (cm-ekben).
A deltoid területe 33 cm2.
A következő Matek Oázis videókkal tanulhatsz a deltoidról
2007. október, I. rész / 1-7. feladat
A 2007-es matekérettségi első 7 feladatának részletes megoldásán vezetünk végig ezen a videón. Közben tréningezünk arra is, hogy minél gyorsabban oldd meg a példákat, hisz az érettségin is nagyon fontos, hogy mennyi idő alatt végzel az I. rész feladataival. Mint mindig, ezek a példák is nagyon különböző témakörökből kerültek ki: volt egy halmazos feladat, aztán törtekkel kellett számolni, majd egy kis trigonometria és logaritmus következett. A 4. feladatban százalékszámítás és valószínűség keveredett, majd számelmélet kérdések jöttek, és egy deltoidra vonatkozó állítás. Aztán egy érdekes logaritmusos egyenletet kellett megoldani, a 7. feladatban pedig egy számtani sorozat első 5 tagjának összegére kérdeztek rá.
Négyszögek szerkesztése - négyzet, téglalap, rombusz
Speciális négyszögek szerkesztése. Ebben a videóban négyszögek szerkesztését tanuljuk meg. Körzővel és vonalzóval szerkesztjük meg a négyzetet, téglalapot, rombuszt. Az alapos begyakorláshoz ceruzára, papírra, vonalzóra és körzőre is szükséged lesz.
Négyszögek szerkesztése - trapéz, deltoid
Speciális négyszögek szerkesztése - folytatás. Folytatjuk a négyszögek szerkesztését. Körzővel és vonalzóval szerkesztünk rombuszt, szimmetrikus trapézt (húrtrapéz), deltoidot. Az alapos begyakorláshoz ceruzára, papírra, vonalzóra és körzőre is szükséged lesz.
















