Trigonometriai összefüggések
Összefüggések egy szög különböző szögfüggvényei között:
Szög koszinusza egyenlő pótszögének szinuszával.
Szög tangense egyenlő pótszögének kotangensével.
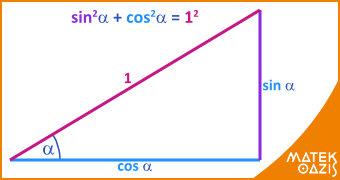
Pitagoraszi azonosság: Adott szög szinuszának és koszinuszának négyzetösszege 1-gyel egyenlő.
A trigonometrikus pitagoraszi összefüggés bizonyítása hegyesszögek esetére az ábrán látható:
Két szög összegének szögfüggvényei (addíciós tételek):
Példák trigonometriai összefüggések alkalmazására
1. feladat: Az ɑ hegyesszögre sin (ɑ) = 0,3. Számítsuk ki 3 tizedesjegy pontossággal ɑ koszinuszát és tangensét, anélkül, hogy ɑ-t meghatároznánk!
Megoldás: Az ɑ koszinuszát a Pitagoraszi azonosságot átalakítva kapjuk meg:
A tangenst a szinusz és a koszinusz segítségével számoljuk ki:
2. feladat: Adjuk meg ɑ hegyesszög nagyságát, ha 
Megoldás: Felhasználjuk, hogy hegyesszög koszinusza egyenlő pótszögének szinuszával: 
.
Ezt behelyettesítve az eredeti egyenlet baloldalára, azt kapjuk, hogy, 
, ebből látszik, hogy:
A feladat szövege hegyesszöget kérdez, ezért nincs más megoldás. Ha nem csak hegyesszög lehet a megoldás, akkor figyelni kell a nem hegyesszögű megoldásra, illetve a priódusokra is gondolni kell.
A következő Matek Oázis videókkal tanulhatsz a trigonometriai összefüggésekről
Trigonometrikus egyenlőtlenségek
Az egyenletek után a trigonometrikus egyenlőtlenségek megoldásával is foglalkozunk. Tisztázzuk a tudnivalókat a nevezetes szögekről, meghatározzuk a tartományt, a periódust, amiben számolunk. Szinusz, koszinusz, tangens, kotangens szögfüggvényekkel is dolgozunk. Feladatokat oldunk meg a trigonometrikus egyenlőtlenségek megoldásának gyakorlására.
2005. október, I. rész / 1-8. feladat
Ezen a videón a 2005.októberében megírt matek érettségi feladatok megoldásait nézzük át, az első 8 feladatét. Nagyon sok témakörből vették a példákat: algebrai tört egyszerűsítése, számelmélet(oszthatósági szabályok), trigonometria (szögfüggvények derékszögű háromszögekben),egyenes egyenlete, törtes egyenlőtlenség, algebra, vektorok. Oldjuk meg együtt ezeket a feladatokat!
2009. okt.: I. rész 1-12. feladat
Matematika októberi érettségi feladatsor I. rész12 feladata megoldásokkal: Számtani,mértani közép; Halmazos; Valószínűségszámítás; Exponenciális egyenlet; Szögfüggvény alkalmazása derékszögű háromszögben; Mértani sorozat; Függvény hozzárendelési szabálya; Logaritmusos egyenlet; Térgeometria; Trigonometria feladat
Hegyesszögek szögfüggvényei
JÁTÉK! Telepítsd be a tengeri akváriumot! Derékszögű háromszögekben keressük az alfa vagy a béta szög szögfüggvényeit. El kell döntened, hogy a felírt tört a megadott szög szinuszával, koszinuszával, vagy épp tangensével-kotangensével egyezik meg. Látni fogod utána a magyarázatot is, így a végére már magabiztosan fogod tudni használni a szögfüggvényeket.
2019. okt. 1-12. feladat
Oldjuk meg közösen a 2019-es októberi érettségi feladatsor első részét: gráfok, halmazok, hatványozás, százalékszámítás, számelmélet, függvények, geometria feladat szögfüggvények alkalmazásával, koordinátageometria, térgeometria és valószínűség. Sokféle témakör szerepel ebben a feladatsorban.
Szintfelmérő 10. oszt. után 1. rész
TESZT! A 10. -es matek mennyire megy? Ellenőrizd a tudásod, oldd meg a feladatokat önállóan! Logikával, állításokkal hogy állsz? Meg tudod oldani a másodfokú és a gyököks egyenleteket? A szögfüggvényekkel boldogulsz? A kombinatorika és a valószínűségszámítás sem fog ki rajtad? Ha jól sikerült a teszt, folytasd a következővel! Ha hiányosságaid vannak, muszáj lenne pótolnod őket, hogy jól tudd venni a 11. osztály akadályait.
Szintfelmérő 11. oszt. után 1. rész
TESZT! A középiskolás matek mennyire megy? Tedd próbára magad, oldd meg a feladatokat önállóan! Tudsz bánni a gráfokkal? Tudsz számolni gyökökkel, hatványokkal? Jóban vagy a függvényekkel, szögfüggvényekkel? Meg tudsz oldani egyenlőtlenségeket? Ha jól sikerült a teszt, folytasd a következővel! Ha hiányosságaid vannak, mindenképpen pótolnod kellene őket, különben gondot okoznak majd az érettségire készülés során.
Szögfüggvények derékszögű háromszögekben - fogalmak
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón!
Szögfüggvények derékszögű háromszögekben
A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón, és gyakoroljunk közösen!
2008. októberi érettségi feladatsor I. rész
Ez a matematikai oktatóvideó a 2008-as októberi matekérettségi I. részének feladatait tekinti át. Mind a 12 feladat részletes, interaktív megoldásaival találkozhatsz, és mivel Te is részt veszel a megoldásban, sokkal többet tanulhatsz belőle, mintha csak végignéznéd azt. Volt a példák között számelmélet, hasonlóság, halmazok, vektorok, sin-cos derékszögű háromszögben, statisztika, geometriai állítások, és trigonometrikus összefüggések is. Oldd meg velünk ezeket a példákat!
7. Másodfokú egyenletek, egyenlőtlenségek
7. tétel: Másodfokú egyenletek és egyenlőtlenségek. Másodfokúra visszavezethető egyenletek. Egyenletek ekvivalenciája, gyökvesztés, hamis gyök, ellenőrzés. Megmutatjuk a teljes kidolgozott tételt, úgy, ahogyan a vizsgán elmondhatod. Közben látni fogod, hogy mit érdemes a táblára írni. A videó második felében segítünk, hogy gyorsan meg is tudd tanulni a tételt. Mi az egyenlet, mit jelent az egyenlet alaphalmaza, értelmezési tartománya, illetve az egyenlet megoldásai? Ha két algebrai kifejezést egyenlőségjellel kapcsolunk össze, egyenletet kapunk. Az egyenlet leírásában egy vagy több változó szerepel. Az egyenlet megoldása során a változónak vagy változóknak azokat az értékeit keressük meg, amelyekre az egyenlet igaz logikai értéket vesz fel. Ez(ek) az egyenlet megoldásai vagy gyökei Minden egyenletnek van egy alaphalmaza, és ennek egy részhalmaza az értelmezési tartomány. Az értelmezési tartomány az alaphalmaznak azon legbővebb részhalmaza, amelyen az egyenletben szereplő összes algebrai kifejezés értelmezve van. Amennyiben nem adunk meg mást, a valós számok halmazát tekintjük alaphalmaznak. Ha az értelmezési tartomány minden elemére igaz lesz az egyenlet, akkor azt mondjuk, hogy az az egyenlet azonosság. Ha egyetlen értelmezési tartománybeli elemre sem igaz az egyenlet, akkor az egyenletnek nincs megoldása. Egy másik megközelítés szerint az egyenlet mindkét oldala egy-egy függvény hozzárendelési szabálya. Az egyenlet megoldása során pedig azokat az értelmezéstartománybeli -eket keressük, amelyekre a két függvény felvett függvényértéke megegyezik. Amennyiben grafikus úton oldjuk meg az egyenletet, a két függvény metszéspontjának vagy metszéspontjainak koordinátája lesz a keresett megoldás. Melyek a másodfokú egyenletek, és hogyan oldjuk meg őket? A másodfokú egyenletek kanonikus, vagy nullára rendezett alakja: ax2 + bx + c = 0 alakú, ahol a, b és c valós paraméterek. Ők az úgynevezett együtthatók, x pedig a változó. Az a értéke nem lehet 0, hiszen akkor nem lenne x2 -es tag, tehát az egyenlet nem lenne másodfokú. Tétel: ax2 + bx + c = 0 alakú, (a nem 0) másodfokú egyenlet megoldásait az x1,2 =…. (másodfokú egyenlet megoldóképlete) képlettel kaphatjuk meg. A bizonyítás lépéseit a videón láthatod. A másodfokú egyenlet megoldásainak a száma a diszkriminánstól függ. A diszkrimináns a megoldóképletben a gyök alatt látható kifejezés. Ha D < 0, nincs valós gyök, ha D = 0, két egybeeső valós gyök van, ha D > 0, két különböző valós gyök van. Feladat: x2 + 6x + 8 = 0 egyenletet megoldjuk a megoldóképlettel. Hogyan kell megoldani paraméteres másodfokú egyenleteket? Paraméteres másodfokú egyenletek esetén gyakran a paramétert a gyökök számára vagy tulajdonságára megadott adat alapján kell meghatározni. Példa: px2 + 4x + p = 0 egyenletben p a paraméter, x az ismeretlen. Ha pl. az a kérdés, hogy a p paraméter milyen értékei mellett lesz egy megoldása ennek az egyenletnek, akkor ezt a diszkrimináns vizsgálatával lehet megválaszolni. D = 0 -ból kapunk p-re egy összefüggést, annak a megoldásait kell keresni. Gyökök és együtthatók közötti összefüggések felírása, gyöktényezős alak, Viete-formulák. Ha az ax2 + bx + c = 0 másodfokú egyenletnek létezik valós gyöke, akkor a másodfokú kifejezés elsőfokú tényezők szorzatára bontható a gyöktényezős alak segítségével. ax2 + bx + c = a ( x - x1 )( x - x2 ) A Viete-formulák a gyökök és együtthatók közt teremtenek kapcsolatot: x1 + x2 = -b/a ; és x1*x2 = c/a A Viete-formulákat és a gyöktényezős alakot is könnyen igazolhatjuk, ha az x1 -re és x2 -re kapott megoldóképletet behelyettesítjük az összefüggésekbe. A Viete-formulák és a gyöktényezős alak is számos feladat megoldását könnyíti meg. Például nem negatív diszkrimináns esetén szorzat alakba tudjuk írni a másodfokú számlálót vagy nevezőt, így egyszerűsíteni tudunk az azonos tényezőkkel. A másodfokú egyenlőtlenség megoldásának lépései. Ha másodfokú egyenlőtlenséget akarunk megoldani, akkor általában grafikus módon fejezzük be a feladatmegoldást, miután a megoldóképlettel a gyököket meghatároztuk. A másodfokú hozzárendelés képe parabola, a kiszámított gyökök a parabola zérushelyei. Két egybeeső valós gyök esetén a parabola érinti az x tengelyt, ha nincs valós gyök, akkor pedig a másodfokú kifejezés minden x-re pozitív vagy minden x-re negatív értéket vesz fel. A parabola ábrázolása után az egyenlőtlenség megoldásai leolvashatók a garfikonról. Melyek a másodfokúra visszavezethető egyenletek és hogyan oldjunk meg őket? Ha egy kifejezés és ugyanannak a kifejezésnek a négyzete szerepel az egyenletben, akkor az adott kifejezésre érdemes új ismeretlent bevezetünk. Mert így az új ismeretlenre nézve lesz másodfokú az egyenlet vagy az egyenlőtlenség. Ezek az egyenletek, egyenlőtlenségek eredeti formájukban lehetnek például magasabb fokúak, logaritmusosok, trigonometrikusak vagy akár összetettebb algebrai kifejezésre nézve másodfokúak. Megnézünk néhány példát is. Mikor ekvivalens az egyenlet átalakítása? Mikor fordulhat elő gyökvesztés illetve hamis gyök? Miért és mikor kell ellenőrizni az egyenlet megoldását? Nagyon fontos, hogy az egyenletek, egyenlőtlenségek megoldásánál mindig figyeljük, hogy ekvivalens, vagy nem ekvivalens a végrehajtott lépés, vagyis azt, hogy a lépések következtében az újabb és újabb egyenlet ekvivalens-e az előző lépésben szereplő egyenlettel. Két egyenlet akkor ugyanaz, ha értelmezési tartomány a és megoldáshalmaza is ugyanaz. Ekvivalens átalakításokra és nem ekvivalensekre is mutatunk példákat. Ha az átalakítás során megváltozik az egyenlet értelmezési tartománya, gyököt veszíthetünk, de akár hamis gyökök is jöhetnek be. A hamis gyököket lehet kizárni ellenőrzéssel. A másodfokú egyenletek, összefüggések alkalmazására mutatunk példákat a tétel végén.