Szögfüggvények (hegyeszszögek szögfüggvényei)

Legyen α egy tetszőleges derékszögű háromszög egyik hegyesszöge. Ekkor az α szög szögfüggvényeinek definíciója:

$sin open parentheses alpha close parentheses equals fraction numerator s z ö g g e l space s z e m k ö z t i space b e f o g ó over denominator á t f o g ó end fraction equals a over c$

$cos open parentheses alpha close parentheses equals fraction numerator s z ö g space m e l l e t t i space b e f o g ó over denominator á t f o g ó end fraction equals b over c$

$tan open parentheses alpha close parentheses equals fraction numerator s z ö g g e l space s z e m k ö z t i space b e f o g ó over denominator s z ö g space m e l l e t t i space b e f o g ó end fraction equals a over b$

$c t g open parentheses alpha close parentheses equals fraction numerator s z ö g space m e l l e t t i space b e f o g ó over denominator s z ö g g e l space s z e m k ö z t i space b e f o g ó end fraction equals b over a$

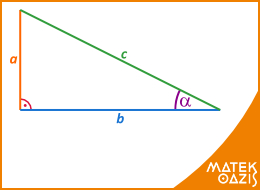
derékszögű háromszög szögfüggvény

A derékszögű háromszögben befogónak nevezzük azokat az oldalakat, amik derékszöget zárnak be egymással. A leghosszabb oldal neve átfogó.

$sin open parentheses alpha close parentheses space$ jelölése egyszerűen : $sin space alpha$ , és a többi szögfüggvény esetén is elhagyható a zárójel.

Tetszőleges $alpha$ forgásszögre és $k$ egész számra:

$sin open parentheses alpha close parentheses equals sin open parentheses alpha plus k times 360 degree close parentheses$ trigonometriai összefüggések

$cos open parentheses alpha close parentheses equals cos open parentheses alpha plus k times 360 degree close parentheses$

$t g left parenthesis alpha right parenthesis equals t g left parenthesis alpha plus k times 180 degree right parenthesis$

$c t g left parenthesis alpha right parenthesis equals c t g left parenthesis alpha plus k times 180 degree right parenthesis$

Példa a szögfüggvények megértéséhez

Feladat: Egy derékszögű háromszögben jelölje a és b a befogók hosszát, c pedig az átfogó hosszát. α legyen az a hosszúságú befogóval szemközti szög, számítsuk ki α szinuszát koszinuszát, tangensét és kotangensét, ha
a = 6, b = 8.

Megoldás: Felhasználjuk az ábrát, ami a definíciók mellett található.Mindkét esetben először meg kell határoznunk a harmadik, c oldal hosszát. Ehhez Pitagorasz-tétel használunk. Az első esetben 6² + 8² = c², azaz 36 + 64 = c². Ebből 100 = c² és így c = 10. A szögfüggvények meghatározásához behelyettesítünk a megfelelő összefüggésekbe.

$sin space alpha space equals fraction numerator s z ö g g e l space s z e m k ö z t i space b e f o g ó over denominator á t f o g ó end fraction equals a over c equals 6 over 10 equals 0 comma 6$

$cos space alpha equals fraction numerator s z ö g space m e l l e t t i space b e f o g ó over denominator á t f o g ó end fraction equals b over c equals 8 over 10 equals 0 comma 8$

$tan space alpha space equals fraction numerator s z ö g g e l space s z e m k ö z t i space b e f o g ó over denominator s z ö g space m e l l e t t i space b e f o g ó end fraction equals a over b equals 6 over 8 equals 0 comma 75$

$c t g space alpha equals fraction numerator s z ö g space m e l l e t t i space b e f o g ó over denominator s z ö g g e l space s z e m k ö z t i space b e f o g ó end fraction equals b over a equals 8 over 6 equals 1 comma 3 with dot on top$

A szögfüggvények általánosításáról (szögfüggvények tetszőleges valós számokon) az emelt szintű videókból tanulhatsz (ld. lejjebb).

A következő Matek Oázis videókkal tanulhatsz a szögfüggvényekről

Szögfüggvények derékszögű háromszögekben

Teszt

TESZT! Hét feladat megoldásával gyakorolhatod a szögfüggvények használatát derékszögű háromszögekben. Oldd meg a feladatokat önállóan! Kiértékelés után levezetjük a megoldást lépésről lépésre.

1. feladatsor

Tananyag

Egyenletek: másodfokú, gyökös, törtes, trigonometrikus egyenletek; Geometriai feladat: magasságtétel és szögfüggvény használata; szabályos tízszög oldala, területe

Trigonometrikus egyenletek - gyakorlás

Tananyag

Trigonometrikus egyenletek megoldását gyakorolhatod velünk további tíz feladat megoldásával. A szinusz, koszinusz, tangens, kotangens szögfüggvények összefüggéseit alkalmazva megmutatjuk a típusfeladatokat és a megoldásuk mesterfogásait.

Trigonometrikus egyenlőtlenségek

Tananyag

Az egyenletek után a trigonometrikus egyenlőtlenségek megoldásával is foglalkozunk. Tisztázzuk a tudnivalókat a nevezetes szögekről, meghatározzuk a tartományt, a periódust, amiben számolunk. Szinusz, koszinusz, tangens, kotangens szögfüggvényekkel is dolgozunk. Feladatokat oldunk meg a trigonometrikus egyenlőtlenségek megoldásának gyakorlására.

2005. október, I. rész / 1-8. feladat

Tananyag

Ezen a videón a 2005.októberében megírt matek érettségi feladatok megoldásait nézzük át, az első 8 feladatét. Nagyon sok témakörből vették a példákat: algebrai tört egyszerűsítése, számelmélet(oszthatósági szabályok), trigonometria (szögfüggvények derékszögű háromszögekben),egyenes egyenlete, törtes egyenlőtlenség, algebra, vektorok. Oldjuk meg együtt ezeket a feladatokat!

2009. okt.: I. rész 1-12. feladat

Tananyag

Matematika októberi érettségi feladatsor I. rész12 feladata megoldásokkal: Számtani,mértani közép; Halmazos; Valószínűségszámítás; Exponenciális egyenlet; Szögfüggvény alkalmazása derékszögű háromszögben; Mértani sorozat; Függvény hozzárendelési szabálya; Logaritmusos egyenlet; Térgeometria; Trigonometria feladat

2010. májusi érettségi feladatsor I. rész

Tananyag

Rövid választ igénylő 12 matematika érettségi feladat: Oszthatóság; Másodfokú egyenlet; Átlag; Logaritmus; Kombinatorika; Szögfüggvény alkalmazása; Gráf; Valószínűségszámítás; Trigonometrikus egyenlet; Igaz-hamis; Kombinatorika feladatok

Szögfüggvények és alkalmazásuk

Teszt

TESZT! Gyakorold a szögfüggvények alkalmazását! Feladatok, melyek megoldásával letesztelheted mennyire sikerült elsajátítanod a szögfüggvényekről tanultakat. Keresd meg a rajzokon a derékszögű háromszögeket, és írd fel a szögek szögfüggvényeit!

Hegyesszögek szögfüggvényei

Játék

JÁTÉK! Telepítsd be a tengeri akváriumot! Derékszögű háromszögekben keressük az alfa vagy a béta szög szögfüggvényeit. El kell döntened, hogy a felírt tört a megadott szög szinuszával, koszinuszával, vagy épp tangensével-kotangensével egyezik meg. Látni fogod utána a magyarázatot is, így a végére már magabiztosan fogod tudni használni a szögfüggvényeket.

TESZT! Hegyesszögek szögfüggvényei

Teszt

TESZT! Keresd a derékszögű háromszögeket, és a szögfüggvények segítségével határozd meg a hiányzó oldalakat, szögeket! Dolgozz önállóan, majd ellenőrizd a magad! Kiértékelés után láthatod a részletes megoldásokat!

2019. okt. 1-12. feladat

Tananyag

Oldjuk meg közösen a 2019-es októberi érettségi feladatsor első részét: gráfok, halmazok, hatványozás, százalékszámítás, számelmélet, függvények, geometria feladat szögfüggvények alkalmazásával, koordinátageometria, térgeometria és valószínűség. Sokféle témakör szerepel ebben a feladatsorban.

Szintfelmérő 10. oszt. után 1. rész

Teszt

TESZT! A 10. -es matek mennyire megy? Ellenőrizd a tudásod, oldd meg a feladatokat önállóan! Logikával, állításokkal hogy állsz? Meg tudod oldani a másodfokú és a gyököks egyenleteket? A szögfüggvényekkel boldogulsz? A kombinatorika és a valószínűségszámítás sem fog ki rajtad? Ha jól sikerült a teszt, folytasd a következővel! Ha hiányosságaid vannak, muszáj lenne pótolnod őket, hogy jól tudd venni a 11. osztály akadályait.

Szintfelmérő 11. oszt. után 1. rész

Teszt

TESZT! A középiskolás matek mennyire megy? Tedd próbára magad, oldd meg a feladatokat önállóan! Tudsz bánni a gráfokkal? Tudsz számolni gyökökkel, hatványokkal? Jóban vagy a függvényekkel, szögfüggvényekkel? Meg tudsz oldani egyenlőtlenségeket? Ha jól sikerült a teszt, folytasd a következővel! Ha hiányosságaid vannak, mindenképpen pótolnod kellene őket, különben gondot okoznak majd az érettségire készülés során.

Exponenciális feladatok II.

Tananyag

Ebben a videóban további exponenciális egyenletet találsz szögfüggvényekkel tarkítva, megoldhatsz exponenciális egyenlőtlenségeket, és az exponenciális egyenletre vezető szöveges feladatokat is átézzük, ami általában a kamatos kamat témaköréhez kapcsolódik.

12. Derékszögű háromszögekre vonatkozó tételek ...

Tananyag

Derékszögű háromszögekre vonatkozó tételek. A hegyesszögek szögfüggvényei. Összefüggések a hegyesszögek szögfüggvényei között. A szögfüggvények általánosítása.

Tangens szögfüggvény gyakorlása

Tananyag

Gyakoroljuk feladatokban a tangens szögfüggvényt.

Teszt: Tangens alapok

Teszt

TESZT! Gyakorold a tangens szögfüggvényt! Oldd meg egyedül a feladatokat, és ha készen vagy, az értékelésnél láthatod az ereményedet és a részletes magyarázatokat is.

Trigonometria

Teszt

TESZT! Szinusz, kosziniusz, tangens, kotangens, ezekkel a kifejezésekkel találkozhatsz a trigonometria témakörében. Oldd meg önállóan a feladatokat, kiderüljön, mennyire mennek az ilyen típusú példák. Az értékelés után látni fogod a részletes magyarázatokat.

2022. októberi érettségi feladatsor II. rész 13-15. feladat

Tananyag

A 2022. évi október középszintű érettségi vizsga feladatsor II. részéből a kötelezően megoldandó 13-15. feladat megoldása.

Szögfüggvények derékszögű háromszögekben

Tananyag

A szinusz, koszinusz, tangens és kotangens kifejezések rejtelmeibe vezetünk be ebben a videóban. Definiáljuk, mit is jelent ez a derékszögű háromszögben.

Szögfüggvények derékszögű háromszögekben - feladatok 1.

Tananyag

Feladatokat oldunk meg, melyekben gyakorolhatod a szögfüggvények használatát.

Szögfüggvények derékszögű háromszögekben - feladatok 2.

Tananyag

Gyakoroljuk tovább a derékszögű háromszögben a szögfüggvényeket.

A sin x általánosítása

Tananyag

Ebben a matek tananyagban a szinusz szögfüggvény általánosítását vezetjük be, megnézzük a függvény tulajdonságait és a szinuszos alapegyenleteket. Azt is részletesen elmagyarázzuk, mi is az a radián, mert erre is szükség van a trigonometrikus egyenletek megoldásához.

A sin x általánosítása - radián

Tananyag

Részletesen elmagyarázzuk, mi is az a radián, mert erre is szükség van a trigonometrikus egyenletek megoldásához.

A sin x általánosítása - szinuszfüggvény

Tananyag

Szinuszfüggvény jellemzését nézzük meg. Értelmezési tartomány, értékkészlet, zérushely, paritás. A szinuszfüggvény periodikus függvény.

A sin x általánosítása - gyakorlás

Tananyag

Gyakoroljuk feladatokban, amit a szinusz x általánosításáról tanultunk.

Szögfüggvények derékszögű háromszögekben - fogalmak

Tananyag

A szögfüggvények ismerete nagyon fontos a geometriai számításokban. Derékszögű háromszögek hiányzó adatait a szinusz (sin), koszinusz (cos), tangens (tg), kotangens (ctg) szögfüggvények segítségével könnyedén kiszámíthatjuk. Nézd át mindezt ezen az interaktív oktatóvideón!

Szögfüggvények derékszögű háromszögekben - gyakorlás

Tananyag

Gyakorold velünk a sin, cos, tg, ctg szögfüggvények használatát! Megmutatjuk azt is, hogy milyen alakzatokban találkozhatsz derékszögű háromszögekkel.

Szögfüggvények alkalmazása 1.

Tananyag

Ez a videó a szögfüggvények alkalmazásával foglalkozik. Sorra vesszük a nevezetes (30, 45, 60 fokos) szögek szögfüggvényeit. Alkalmazzuk a szögfüggvényeket sík-és térgeometriai feladatokban.

Szögfüggvények alkalmazása 2.

Tananyag

Ez a videó a szögfüggvények alkalmazásával foglalkozik. Alkalmazzuk a szögfüggvényeket sík-és térgeometriai feladatokban.

Gyakorlás - szögfüggvények általánosítása 1.

Tananyag

Ebben a videóban gyakorló feladatokat találsz a szögfüggvények általánosításáról tanultak ellenőrzésére.

Gyakorlás - szögfüggvények általánosítása 2.

Tananyag

Ebben a videóban további gyakorló feladatokat találsz a szögfüggvények általánosításáról tanultak ellenőrzésére. Háromszög területének kiszámítását gyakorolhatod két oldal és az általuk bezárt szög ismeretében.