Tengelyesen szimmetrikus alakzat
Egy kép vagy alakzat tengelyesen szimmetrikus, ha van olyan egyenes, amire az alakzatot tükrözve önmagába megy át. Ezt az egyenest hívjuk tükörtengelynek vagy szimmetriatengelynek. Leggyakrabban t-vel jelöljük.
Szemléletesen: ha félbe tudjuk hajtani úgy az alakzatot, hogy a hajtásélre egy tükröt helyezve az eredeti kép fele és a tükörkép az eredeti egész képet adja vissza.
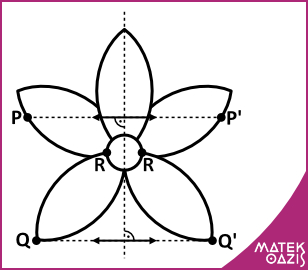
Példák a tengelyesen szimmetrikus alakzatok felismeréséhez
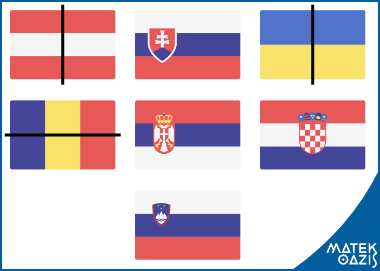
Feladat: Magyarország szomszédai: Ausztria, Szlovákia, Ukrajna, Románia, Szerbia, Horvátország és Szlovénia. Ezeknek az országoknak itt láthatod a zászlóit. Keresd meg melyik zászló tengelyesen szimmetrikus. Ami szimmetrikus azon jelöld is be a szimmetriatengelyt!

Megoldás: A helyes válaszok: Ausztria, Ukrajna, Románia. A tükörtengelyeket is berajzoltuk
A következő Matek Oázis videókkal tanulhatsz a tengelyesen szimmetrikus alakzatokról
Tengelyes- és középpontos tükrözés - tulajdonságok
Ez a videó a következő két geometriai transzformációt mutatja be részletesen: A tengelyes tükrözés és a középpontos tükrözés tulajdonságait vesszük sorba, és feladatokat, amiket ezekkel a transzformációkkal lehet megoldani. A tengelyesen szimmetrikus alakzatok mellett a középpontosan szimmetrikusakat is leltárba vesszük.











