Tengelyes tükrözés
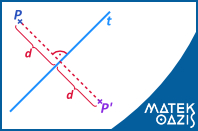
Legyen adott a sík egy t egyenese. A sík összes P pontjához hozzárandeljük a P' pontot a következőképpen:
- Ha P rajta van a t tengelyen, akkor P = P'.
- Ha P nincs rajta a t tengelyen, akkor P' a sík azon pontja, amelyre teljesül, hogy PP' szakasz felező merőlegese a t egyenes.
A t egyenest hívjuk a tükrözés tengelyének.
A pont és a tükörképe a t tükörtengelytől egyenlő távolságra van (tehát azoknak a pontoknak önmaguk a tükörképe, amik a tengelyen vannak).
A pontot és a tükörképét összekötő szakasz merőleges a tengelyre.
A tengelyes tükrözés egy olyan egybevágósági transzformáció, ami távolságtartó, szögtartó, egyenestartó, valamint a tükörkép körüljárási iránya megváltozik.
Egy kép vagy alakzat tengelyesen szimmetrikus, ha félbe tudjuk hajtani úgy, hogy a hajtásélre egy tükröt helyezve az eredeti kép fele és a tükörkép az eredeti egész képet adja vissza. A hajtásélre illeszkedő egyenest hívjuk tükörtengelynek vagy szimmetriatengelynek. Leggyakrabban t-vel jelöljük.

Példa tengelyes tükrözéssel
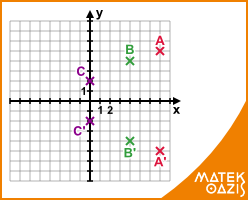
Feladat: Egy háromszög csúcsai a derékszögű koordinátarendszerben: A (7 ; 5), B (4 ; 4), C (0 ; 2). Tükrözzük a háromszöget az x tengelyre!
Megoldás: Ha a vízszintes, x tengelyre tükrözünk, akkor merőlegeseket állítunk az tengelyre. Mivel az y koordináták az x tengelytől való távolságot mutatják meg, csak annyi a dolgunk, hogy az y koordinátákat a (-1)-szeresükre változtatjuk. Így A' (7 ; -5), B' (4 ; -8), C' (0 ; -2). Ezt ábrázolni is nagyon könnyű.
A következő Matek Oázis videókkal tanulhatsz a tengelyes tükrözésről
Tengelyes- és középpontos tükrözés - tulajdonságok
Ez a videó a következő két geometriai transzformációt mutatja be részletesen: A tengelyes tükrözés és a középpontos tükrözés tulajdonságait vesszük sorba, és feladatokat, amiket ezekkel a transzformációkkal lehet megoldani. A tengelyesen szimmetrikus alakzatok mellett a középpontosan szimmetrikusakat is leltárba vesszük.













