Teljes gráf
A gráfok csúcsokból és őket összekötő élekből állnak.
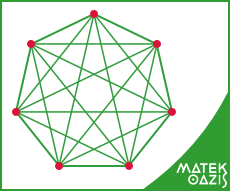
Az olyan gráfokat, ahol minden csúcs össze van kötve minden csúccsal, teljes gráfoknak nevezzük. Ez azt jelenti, hogy az összes lehetséges élet behúzzuk a gráfba.
Az élek száma egy teljes gráfban:
Indoklás: A gráf minden csúcsából a többi (n - 1) csúcshoz húznunk tehát élt. Így elvileg n (n - 1) élt kapnánk, ám ezt osztani kell kettővel, mert különben duplán számolnánk minden élt. Például A és B csúcs között futó élt kétszer számolnánk: egyszer, amikor az A-ból induló éleket nézzük, és egyszer, amikor a B-ből kiinduló éleket.
Példa teljes gráfra
Feladat: Egy 8 tagú baráti társaság találkozik. Érkezéskor mindenki kezet fog mindenkivel. Hány kézfogás történt összesen?
Megoldás: A feladatot tudjuk gráf segítségével ábrázolni. A csúcsok az emberek, az élek a kézfogások. Mivel mindenki kezet fog mindenkivel, ezért ezt egy teljes gráffal tudjuk szemléltetni. A kézfogások (azaz az élek) száma a kérdés, ehhez tudjuk használni a képletet:
Tehát 28 kézfogás történt a találkozó elején.
A következő Matek Oázis videókkal tanulhatsz a teljes gráfról
Halmazok, számelmélet, logika, gráfok
TESZT! Teszteld magad! Meg tudod oldalni a halmazokkal, gráfokkalkapcsolatos feladatokat? Ismered az oszthatósági szabályokat, át tudsz váltani egyik számrendszerből a másikba? És hogy állsz a logikai feladatokkal? Ha megoldod a példákat, minden kiderül, amelyik esetleg nem megy, annak látni fogod a részletes megoldását az értékelés után.











