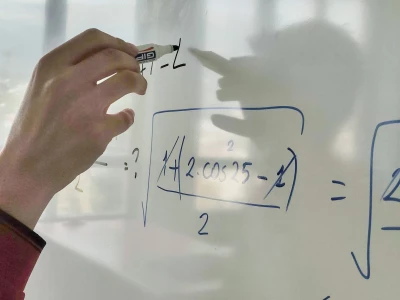Számtani sorozat
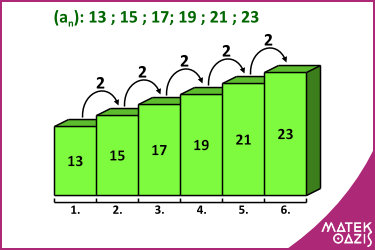
Az an sorozat számtani sorozat, ha van olyan a és d szám, hogy a1 = a és an+1 = an + d , minden n természetes szám esetén.
Ebben a definícióban n azt jelenti, hogy a sorozat hányadik tagjáról van szó (a1 a sorozat első tagja), d a sorozat "különbsége", idegen szóval differenciája.
d megmutatja, hogy a sorozat bármelyik tagja mennyivel nagyobb az előző tagnál (ezért hívjuk d-t különbségnek).
Ha ismerjük a sorozat első tagját és a differenciát, akkor a sorozat bármelyik tagját meg tudjuk határozni:
Ha tudjuk az első tagot és a differenciát, akkor a sorozat első n tagjának az összegét is ki tujduk számolni ezzel a képlettel:
Példa számtani sorozatos feladatra
Feladat: Az an számtani sorozatban a3 = 23 és a4 = 32. Határozzuk meg a sorozat első tagját és a differenciáját! Adjuk meg a sorozat első 10 tagjának az összegét!
Megoldás: Először kiszámoljuk a differenciát, amit úgy kapunk meg, hogy a 4. tagból kivonjuk a 3. tagot: d = a4 - a3 = 32 - 23 = 9.
Az első 10 tag összegéhez tudnunk kell az első tagot. Ezt úgy kapjuk meg, hogy a 3. tagból kivonjuk kétszer a differenciát: a1 = a3 - 2 ·d = 23 - 2 · 9 = 23 - 18 = 5.
Most már be tudunk helyettesíteni mindent az összegképletbe:
A következő Matek Oázis videókkal tanulhatsz a számtani sorozatokról
25. Bizonyítási módszerek...
25. tétel: Bizonyítási módszerek és bemutatásuk tételek bizonyításában. Az utolsó tételt akár viszonylag könnyen meg is úszhatod, és válogathatsz az előző szóbeli tételekből hozzá példákat (ezzel időt spórolhatsz meg.) Mi most megmutatunk Neked másik bizonyításokat is, hogy több bizonyítás lehessen a tarsolyodban, ha szükséged lenne rá. Négyféle bizonyítási módszert használunk középiskolában: a direkt bizonyítást, az indirekt bizonyítást, a teljes indukciót és a skatulya-elvet. Ezeket a módszereket be is mutatjuk tételek bizonyításában. 1. A matematikában leggyakrabban a direkt bizonyítást használjuk. Direkt bizonyításnak nevezzük azt az eljárást, amikor igaz feltételekből például axiómákból vagy korábban bizonyított tételekből, helyes logikai lépések során a bizonyítandó állításhoz jutunk. Thálesz-tételét fogjuk így bizonyítani a videón. A tétel így szól: Ha egy kör egyik átmérőjének két végpontját összekötjük a körvonal átmérővégpontoktól különböző bármely más pontjával, akkor derékszögű háromszöget kapunk. A bizonyításhoz a körben kialakuló egyenlőszárú háromszögeket kell felhasználni. Néhány szögekre vonatkozó összefüggést felírva megkapjuk a bizonyítandó állítást. 2. Hogyan működik az indirekt bizonyítás? Az indirekt módszer két logikai törvényen alapul: minden kijelentés igaz vagy hamis és egy igaz állítás tagadása hamis, és fordítva, hamis kijelentés tagadása igaz. Indirekt bizonyítási módot akkor érdemes választani, ha az állítás tagadása könnyebben kezelhető, mint maga az állítás. A precíz definíció így szól: Indirekt bizonyításnak nevezzük azt az eljárást, amikor feltételezzük a bizonyítandó állítás tagadását, majd helyes logikai lépések során ellentmondásra jutunk. Egy klasszikus, ide tartozó bizonyítás, hogy a gyök kettő irracionális szám (ezt bizonyítjuk a 2. tétel kifejtésekor) Most azonban a Pitagorasz-tétel megfordítását fogjuk bebizonyítani indirekt módon. A Pitagorasz-tétel megfordítása: ha egy háromszögben két oldalhossz négyzetének összege egyenlő a harmadik oldal négyzetével, akkor a háromszög derékszögű. A Pitagorasz tételből tudjuk, hogy a2+b2=c2. Indirekten tegyük fel, hogy ez a háromszög nem derékszögű. Rajzolunk egy általános háromszöget, aminek az oldalai a, b és c. Ezután rajzolunk egy derékszögű háromszöget a, b befogókkal, ez lesz az AB’C háromszög. … A folytatásban belátjuk, hogy a két háromszögnek egybevágónak kell lenni. Evvel viszont ellentmondásra jutunk, hiszen az indirekt feltevésben azt mondtuk, hogy a háromszög nem derékszögű. Ezzel bebizonyítottuk a Pitagorasz-tétel megfordítását. 3. Hogyan kell teljes indukciós bizonyítást levezetni? A teljes indukció olyan állítások bizonyítására alkalmas, melyek n pozitív egész számtól függenek. A teljes indukciós eljárás során először bebizonyítjuk az állítást n = 1-re (vagy valamilyen konkrét értékre). Ezután feltételezzük, hogy az állítás igaz n = k-ra, ez az úgynevezett indukciós feltevés. 3. lépésben az indukciós feltevés felhasználásával bebizonyítjuk, hogy az állítás igaz n = (k + 1)-re. Ezzel az állítást minden n pozitív egész számra bizonyítottnak tekintjük Azt a tételt fogom bizonyítani, hogy Ha egy számtani sorozat első tagja a1, különbsége d, akkor a számtani sorozat első n tagjának összege így számolható, ahogy ide felírtam. A 3 lépés: 1.) megvizsgálom, hogy n=1-re teljesül-e az állítás. Ez könnyen belátható, behelyettesítés és egyszerűsítés után megkapom, hogy az első egy tag összege a1. Ez nyilvánvalóan igaz. 2.) Felírjuk az indukciós feltételt, azaz, hogy n=k-ra teljesül az állítás. Az összefüggésbe n helyére k-t írunk. 3. lépés: Be kell látni, hogy n=k+1-re is teljesül az állítás. Ehhez behelyettesítettjük az eredeti képletbe n helyére k+1-et. És az előző (k-ra vonatkozó) összefüggést felhasználva algebrai átalakításokkal ügyesen kihozzuk a k+1-re vonatkozó összefüggést. A teljes indukció első írásos emléke 1575-ből származik: Ekkor bizonyította be a Maurolico olasz matematikus az első n páratlan szám összegére vonatkozó tételt ilyen módon. 4. A skatulya-elv mit jelent? Tétel: Ha n darab tárgyat k darab skatulyában helyezünk el, és n > kp, akkor biztosan lesz legalább egy olyan skatulya, amelyikbe legalább p + 1 tárgy kerül. Azt a tételt bizonyítjuk be skatulyaelvvel, hogy ha p és q pozitív egész számok, akkor a p/q szám tizedes tört alakja vagy véges, vagy végtelen, de szakaszos tizedes tört. Ha p-t elosztjuk q-val, akkor q féle osztási maradékot kaphatunk. 0-t, 1-t, 2-t és így tovább, egészen q-1-ig. Ezek lesznek a skatulyák, és könnyen belátható, hogy emiatt legfeljebb a q-adik osztásnál már olyan maradékot kapunk, amely korábban már volt, azaz innen ismétlődni fognak a tizedes tört jegyei... A skatulyaelvet Dirichlet (1805–1859) francia matematikus bizonyította be. Gyakorlati alkalmazásként az összes, középiskolában tanult tételt fel lehet hozni, mindegyiket valamelyik fenti módszer segítségével bizonyítottuk. A tétel végén matematikatörténeti vonatkozásokat mutatunk be.