Függvények paritása
Az f függvényt párosnak nevezzük, ha az értelmezési tartomány minden x elemére teljesül a következő két állítás:
1. - x is eleme az értelmezési tartománynak
2. f (- x) = f (x)
A páros függvények grafikonja szimmetrikus az y tengelyre.
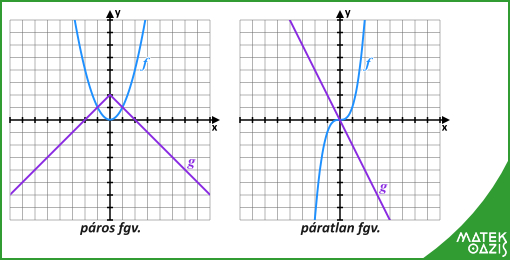
Az f függvényt páratlannak nevezzük, ha az értelmezési tartomány minden x elemére teljesül a következő két állítás:
1. - x is eleme az értelmezési tartománynak
2. f (- x) = - f (x)
A páratlan függvények grafikonja szimmetrikus az origóra.
Ha egy függvény nem páros, akkor abból NEM következik, hogy páratlan. A legtöbb függvény se nem páros, se nem páratlan.
Példák a függvények paritásánának megértéséhez
Példák páros függvényekre: f (x) = x2; x4; | x |; cos( x );
Részletesen nézzük meg az f (x) = x4 függvényt. Az első feltétel teljesül, hiszen a függvény a valós számok halmazán értelmezett. A második feltételt nézzük meg egy táblázat segítségével.
| x | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| f (x) | 0 | 1 | 16 | 81 |
| f (-x) | 0 | 1 | 16 | 81 |
Ezen a táblázaton azt látjuk, hogy az x4 függvény 0-hoz 0-t rendel. 1-hez és mínusz 1-hez is 1-et rendel. 2-höz és -2-höz is 16-ot rendel. 3-hoz és -3-hoz is 81-et rendel. Minden esetben f ( - x ) = f (x), tehát a függvény páros. Ha ábrázoljuk, akkor meg is győzödhetünk róla, hogy a függvény szimmetrikus az y tengelyre.
Példa páratlan függvényekre: f (x) = x; x3; sin ( x );
Részletesen nézzük meg az f (x) = x3 függvényt. Az első feltétel teljesül, hiszen a függvény a valós számok halmazán értelmezett. A második feltételt nézzük meg egy táblázat segítségével.
| x | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| f (x) | 0 | 1 | 8 | 27 |
| f (-x) | 0 | - 1 | -8 | -27 |
Ezen a táblázaton azt látjuk, hogy az x3 függvény 0-hoz 0-t rendel. 1-hez 1-et, mínusz 1-hez - 1-et rendel. 2-höz 8-at rendel, míg -2-höz -8-at. Minden esetben f ( - x ) = - f (x), tehát a függvény páratlan. Ábrázoláskor azt látjuk, hogy a függvény szimmetrikus az origóra.
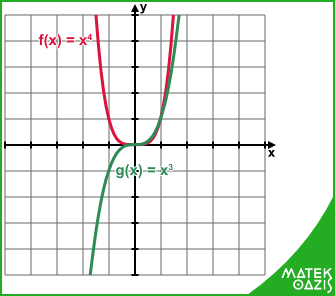
Ezen az ábrán látható, hogy az x4 páros függvény szimmetrikus az y tengelyre, az x3 páratlan függvény pedig az origóra szimmetrikus
A következő Matek Oázis videókkal tanulhatsz a függvények paritásáról
Fontosabb függvények
Ezen a matematikai oktatóvideón a fontosabb függvénytípusokat vesszük sorra: lineáris függvények, másodfokú függvények, hatványfüggvények, abszolútérték-függvény, négyzetgyökfüggvény, és a törtfüggvények. Hogyan kell ábrázolni ezeket a függvényeket? Mi jellemzi őket szélsőérték, monotonitás, zérushely szempontjából, páros vagy páratlan-e a függvény.
Négyzetgyökfüggvény, törtfüggvény
Ez a videó további függvényekkel kapcsolatos ismeretek gyakorlására szolgál. Négyzetgyök-függvény, törtfüggvény. A függvények jellemzését gyakorolhatod ezekkel a feladatokkal. Értelmezési tartomány és értékkészlet, zérushely, növekedés-fogyás (csökkenés), valamint a szélsőértékek (minimum és maximum), sőt: páros és páratlan függvény. Mindegyikkel tisztában vagy, mit jelent?
Egészrész-, törtrész- és előjel-függvény
Az egészrész és törtrész-függvény ábrázolását, a függvények jellemzését gyakorolhatod ezekkel a feladatokkal. Értelmezési tartomány és értékkészlet, zérushely, növekedés-fogyás (csökkenés), valamint a szélsőértékek (minimum és maximum), sőt: páros és páratlan függvény. Mindegyikkel tisztában vagy, mit jelent?
Függvényábrázolás és jellemzés gyakorlása I. rész
Feladatok megoldásával gyakorold a függvények ábrázolását, függvényjellemzést és a függvénytranszformálást. Lineáris függvény, másodfokú függvény, hatványfüggvény, abszolútérték függvény, négyzetgyök függvény, törtfüggvény, páros ás páratlan függvény is előfordul a feladatokban. Segítünk, hogy mindezt megértsd.
Függvényábrázolás és jellemzés gyakorlása II. rész
Függvények ábrázolását, függvényjellemzést és a függvénytranszformálást is tudod gyakorolni ebben a tananyagban. Lineáris függvény, másodfokú függvény, hatványfüggvény, abszolútérték függvény, négyzetgyök függvény, törtfüggvény, páros ás páratlan függvény is előfordul a feladatokban.