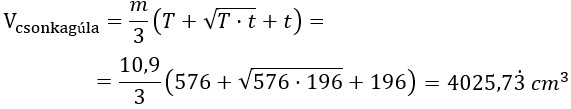Csonkagúla térfogata

Ha egy gúlát az alapjával párhuzamos síkkal elmetszünk, akkor csonkagúlát kapunk.

A csonkagúla térfogatát úgy számolhatjuk ki, hogy az eredeti gúla térfogatából kivonjuk a levágott gúla térfogatát. Figyelembe véve, hogy az eredeti és a levágott gúla hasonlók, levezethető, hogy a következő képletet kapjuk:

V subscript c s o n k a g ú l a end subscript equals space m over 3 open parentheses T plus square root of T times t end root plus t close parentheses                           ahol T az alaplap területe, t a fedőlap területe, m a csonkagúla magassága.

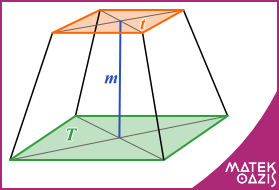
Csonkagúla

Az ábrán egy négyszög alapú csonkagúla látható. A csonkagúla alaplapja bármilyen sokszög lehet.

Példa a csonkagúla térfogatának kiszámítására

Feladat: Egy szabályos négyoldalú csonkagúla alapélének a hossza a = 24 cm, fedőlapjáé c = 14 cm, az oldaléle pedig b = 13 cm. Mekkora a csonkagúla térfogata?

Talaplap = a2 = 242 = 576 cm2

tfedőlap = c2 = 142 =196 cm2​​​​​​​

Négyzet alapú csonkagúla

A csonkagúla magasságának kiszámításához rajzoljuk le a csonkagúlának azt a síkmetszetét, ami átmegy az alapok párhuzamos átlóin!

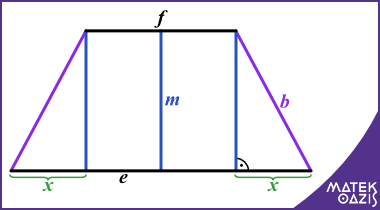
Csonkagúla síkmetszet

Az ábrán a magasságok két derékszögű háromszöget vágnak le a trapézból. Ezeknek az átfogója az oldalél, 13 cm, egyik befogója a magasság, a másik befogó pedig  x space equals space fraction numerator e minus f over denominator 2 end fraction.

Az e szakasz az alap négyzet átlója, ami Pitagorasz-tétellel meghatározható: 24 squared space plus space 24 squared equals space e squared space rightwards arrow space e space equals space 33 comma 9 space c m

Az f szakasz a fedő négyzet átlója, hasonlóan meghatározható:  14 squared space plus space 14 squared space equals space f squared space rightwards arrow space f space equals space 19 comma 8 space c m

A kis háromszög másik befogója tehát: x space equals fraction numerator 33 comma 9 minus 19 comma 8 over denominator 2 end fraction equals space 7 comma 05 space c m

A kis háromszögben felírva a Pitagorasz tételt: 7 comma 05 squared space plus space m squared space equals space 13 squared space rightwards arrow space m space equals space 10 comma 9 space c m

Behelyettesíthetünk a térfogat képletbe:

A kövekező Matek Oázis videókkal tanulhatsz a csonkagúla térfogatáról

Kúp, csonkakúp, csonkagúla

Kúp, csonkakúp, csonkagúla

Ismételjük át, amit tudni kell a kúpról, a csonkakúpról és a csonkagúláról. Hogyan kell kiszámolni a felszínüket, térfogatukat, milyen a palástjuk. Feladatokon gyakorolhatod ezeket az ismereteket.
Térgeometria 2.

Térgeometria 2.

Megoldunk még néhány feladatot a térgeometria témaköréből, számolunk csonkagúlával, oktaéderrel és hengerrel kapcsolatban, megbeszéljük, mit kell tudni a szabályos testekről.
2021. október 13-15. feladat

2021. október 13-15. feladat

A 2021. évi októberi érettségi második részének elejét oldjuk meg, a 13-15. feladatot. Gyakorolhatod a szöveges feladat megoldását, ki kell számolnod a gúla és csonkagúla felszínét, térfogatát, és jó ha tisztában vagy a gráfokkal és a valószínűségszámítással is.
Csonkagúla, csonkakúp

Csonkagúla, csonkakúp

A csonkagúla, csonkakúp tulajdonságai felszíne, térfogata; Feladatok a csonkagúla és a csonkakúp térfogat és felszínszámítás gyakorlásához.
Csonkagúla, csonkakúp - gyakorlás

Csonkagúla, csonkakúp - gyakorlás

További feladatok a csonkagúla és a csonkakúp térfogat és felszínszámítás gyakorlásához.