Algebrai tört
Az algebrai kifejezések azok a kifejezések a matematikában, amik számokat és betűket is tartalmaznak. Ezeknek egy speciális fajtája az algebrai tört.
Egy algebrai kifejezés akkor algebrai tört, ha a tört nevezőjében szerepel ismeretlen (azaz van betű a tört nevezőjében).
Például: vagy
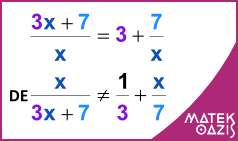
Algebrai törtekkel különböző műveleteket végezhetünk, csakúgy, mint az egyszerű törtekkel.
Nagyon fontos, hogy minden olyan feladatot, amiben algebrai tört szerepel, kikötéssel kezdünk: Mivel nullával nem lehet osztani, meg kell vizsgálni, hogy a tört nevezője az ismeretlen milyen értékei mellett egyenlő 0-val, és ezeket az értékeket ki kell zárni.
Példa az algebrai törtek gyakorlásához
Feladat: Végezzük el a következő műveletet:
Megoldás: Legelső lépés, hogy kikötést teszünk, mert látjuk, hogy a tört nevezőjében ismeretlen van, és az ott lévő kifejezés nem lehet 0.
Kikötés: a -1 ≠ 0, tehát a ≠ 1. Ezenkívül 4a ≠ 0, azaz a ≠0.
Észrevesszük, hogy mindkét tört számlálójából ki tudunk emelni. Ekkor azt kapjuk, hogy
Tudunk egyszerűsíteni keresztben 2-vel, illetve (a-1)-gyel. Ekkor annyi marad a kifejezésből, hogy
Törtet törttel pedig úgy szorzunk, hogy számlálót a számlálóval, nevezőt a nevezővel, így a végeredmény:
A következő Matek Oázis videókkal tanulhatsz az algebrai törtekről
Mérlegelv - haladó feladatok
A mostani matekvideóban gyakorolhatod az egyenletek megoldását a mérlegelv segítségével. Ezek között már nehezebb egyenletek is vannak, és alkalmaznod kell mindazt, amit a nevezetes azonosságokról és az algebrai törtek átalakításairól megtanultál. Tarts velünk, hogy az egyenletrendezésben megfelelő jártasságot szerezhess!
Az algebrai törtek - gyakorlás
Gyakoroljuk az algebrai törtek átalakításait! Az algebrai törteket is közös nevezőre kell hozni, ha összeadni vagy kivonni akarjuk őket. Szorzás és osztás esetén is a törtekhez hasonlóan járunk el. Több feladattal gyakorlunk, hogy végül az ilyen törtes kifejezések se fogjanak ki rajtad.
Gyakorlás (9. osztály) Algebrai törtek
Gyakoroljuk az algebrai törtek egyszerűsítését, algebrai törtek szorzását, osztását, összeadását, kivonását. Az algebrai törtek számlálójában és nevezőjében is betűs kifejezések vannak. Feladatokkal gyakoroljuk a műveletvégzést az algebrai törtekkel. Egyszerűsítsd a törtet! Alakítsd szorzattá!














