Két pont távolsága a koordinátarendszerben
Legyen adott két pont a derékszögű koordinátarendszerben: A (x1 ; y1) és B (x2 ; y2).
Ekkor a két pont d-vel jelölt távolsága:
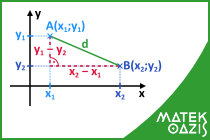
Ha megnézzük az ábrát láthatjuk, hogy egy derékszögű háromszög átfogója a távolság, emiatt számolunk így (Pitagorasz-tétel).
Példa két pont távolságának kiszámítására
Feladat: Adott két pont: A (7 ; 3) és B (4 ; -1). Határozzuk meg a két pont távolságát!
Megoldás: Behelyettesítjük a megfelelő koordinátákat az összefüggésbe:
A következő Matek Oázis videókkal tanulhatsz két pont távolságáról a koordinátarendszerben:
21. Térelemek távolsága és szöge ...
21. tétel: Térelemek távolsága és szöge. Térbeli alakzatok. Felszín- és térfogatszámítás. A videóban látni és hallani fogsz egy kidolgozott, ötös feleletet ebből a tételből. Kékkel mutatjuk azokat, amiket felelet közben felírnánk a táblára. A végén pedig segítünk megtanulni a tételt. Mik azok a térelemek, és mit jelent a távolságuk? A pont, egyenes és sík azok az alapfogalmak, amiket együtt térelemeknek nevezünk. Két térelem illeszkedő, ha egyik részhalmaza a másiknak. Megmutatjuk, mikor illeszkedik egy pont egy egyenesre; egy félegyenes egy egyenesre, illetve egy egyenes egy síkra. Két egyenest metszőnek nevezünk, ha pontosan egy közös pontjuk van. Két egyenes párhuzamos, ha van olyan sík, amelyre mindkettő illeszkedik, de nem metszik egymást. Két egyenest kitérőnek hívunk, ha nincs olyan sík, amelyre mindkettő illeszkedik. Két síkot metszőnek nevezünk, ha pontosan egy közös egyenesük van. Két síkot párhuzamosnak nevezünk, ha nem metszik egymást. Egy egyenest és egy síkot metszőnek nevezünk, ha pontosan egy közös pontjuk van. Egy egyenest és egy síkot párhuzamosnak nevezünk, ha nincs közös pontjuk. Két illeszkedő vagy metsző térelem távolsága 0. A továbbiakban végigvesszük két pont távolságát, pont és egyenes, pont és sík távolságát; majd a különböző helyzetű egyenesek távolságát. Síkok távolságának eseteivel és egyenes és sík távolságának eseteivel is részletesen foglalkozunk. A térelemek szögét hogyan határozhatjuk meg? Egy síkban ugyanabból a pontból kiinduló félegyenest és az általuk meghatározott bármelyik síkrészt szögnek nevezzük. A szög szárai a félegyenesek, a síkrész pedig a szögtartomány. Illeszkedő vagy párhuzamos térelemek szöge 0°. Egyenesek hajlásszöge: Két metsző egyenes 4 szöget határoz meg melyek közül 2-2 egyenlő nagyságú. Ha a két egyenes merőleges egymásra, akkor az általuk bezárt szög 90°. Ha a két egyenes nem merőleges egymásra, akkor az általuk bezárt szög, azaz a két egyenes hajlásszöge a két fajta szög közül a kisebbik. Összességében elmondhatjuk, hogy két egyenes hajlásszöge sosem nagyobb 90°-nál. Két kitérő egyenes hajlásszöge megegyezik a tér bármely pontján átmenő és az adott egyenessekkel párhuzamos egyenesek hajlásszögével. Sík és egyenes hajlásszöge: Ha az e egyenes metszi az S síkot, akkor az egyenes merőleges vetülete a síkon szintén egy egyenes, ezt jelöltem e’-vel. Ilyenkor a sík és egyenes hajlásszöge e és e’ egyenesek hajlásszöge. Megjegyezném, hogy ez a szög a legkisebb a sík egyenesei és az egyenes által bezárt szögek között. Két sík hajlásszöge: Ha két sík nem párhuzamos egymással, akkor metszésvonaluk egy pontjában mindkét síkban merõlegest állítunk a metszésvonalra. A két sík hajlásszöge e két egyenes hajlásszögével egyenlõ. Ez a szög a pont megválasztásától független. Mit nevezünk testnek a geometriában, és milyen speciális testekről tanultunk? A térnek véges felületekkel határolt részét testnek nevezzük. A sokszöglapokkal határolt testek a poliéderek. Például a kocka, vagy a gúla. A szabályos testekre is külön kitérünk a tételben. Definiáljuk a hengerszerű testeket, majd a hengert és a hasábot. A hengerszerű testeken kívül vannak még kúpszerű testek. Definiáljuk még a kúpot és a gúlát, az egyenes kúpot, ill. az egyenes gúlát. A csonkakúpszerű testekről is beszélünk. A térbeli alakzatok kapcsán az utolsó definíció a gömbfelületé. Miket kell elmondani a testek felszínéről? A poliéder felszíne az őt határoló véges számú sokszöglap területének az összege, amit A betűvel jelölünk. Nem poliéderek esetén, ha a test felülete síkba kiteríthető, akkor ennek a területe adja a sík felszínét. Ha a testnek van síkba ki nem teríthető felülete is (például félgömb), akkor ezek felszínét a beírt és köré írt poliéderek felszínének (megegyező) határértékeként értelmezzük. Forgástestek felszínét integrálszámítással is meg tudjuk határozni. A leggyakrabban használt felszín képletek közül néhányat ismertetünk. Mit kell tudni emelt szinten a testek tréfogatáról? A poliéder térfogata egy, a poliéderre jellemző szám, amely a következő 3 tulajdonsággal rendelkezik: Az egységkocka térfogata 1. Az egybevágó poliéderek térfogata egyenlő. A harmadik tulajdonság pedig, ha egy poliédert részpoliéderekre vágunk szét, akkor a részek térfogatának összege egyenlő az egész poliéder térfogatával. Ismertetünk néhány poliéder térfogatának kiszámolásához szükséges képleteket is a tétel kifejtése közben. Eukleidész az Elemek című művében a geometriát axiomatikusan építette fel, azaz a szemléletre hagyatkozva alapfogalmakat, azaz axiómákat határozott meg, és ezek segítségével bizonyított állításokat. A hasábok, gúlák, gömb térfogatának vizsgálatára a kimerítés módszerét (beírt és körülírt hasábok térfogatával való közelítést) használta. Vizsgálta az öt szabályos testet, meghatározta térfogatukat, bebizonyította, hogy csak öt szabályos test létezik. Forgástestek térfogatát az analízis módszereivel tudjuk meghatározni. Ezek kiszámításáról szól a következő tétel. Ha f(x) függvény az [a;b] intervallumon folytonos és f(x) nem negatív, akkor az f(x) függvény grafikonjának az x tengely körüli megforgatásával keletkezett forgástest térfogata kiszámolható a függvény négyzetének integrálásával, a videóban részletezett módon. Ennek segítségével bizonyítható pl. a gömb térfogatának képlete. Még egy tételt érdemes említeni a térfogatokkal kapcsolatban: Hasonló testek térfogatának aránya megegyezik a hasonlóság arányának köbével. Ezeket a geometriai ismereteket alkalmazzák a térképészetben és földmérésben távolság- és szögmérésre. Az építészmérnöki munkában, fizika feladatok megoldása során.