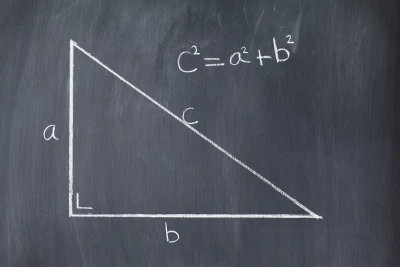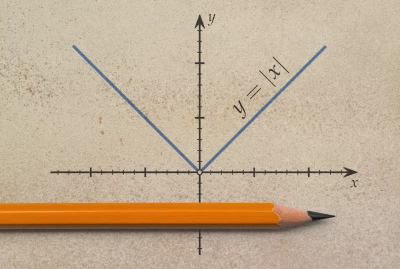Matematika 8. osztály
A teljes 8.-os matek
Számoljunk! (Törtek, negatív számok, műveletek)
3. Egész számok
4. Törtek
5. Tizedestörtek
Mértékegységek
6. Mértékegységek átváltása, hosszúság, terület, térfogat mértékegységei
7. Űrtartalom, tömeg, idő, szög mértékegységei, gyakorlás
Algebrai kifejezések
8. Műveletek betűs kifejezésekkel
9. Hatványozás
10. Gyökvonás
Egyenletek, egyenlőtlenségek, szöveges feladatok
11. Egyenletek
12. Egyenlőtlenségek
13. Szöveges feladatok
Arányosság, százalék
14. Arányosságok
15. Százalékszámítás
Kombinatorika, valószínűség, halmazok
16. Halmazok
17. Kombinatorika
18. Valószínűség
Síkgeometria
19. Háromszögek, négyszögek, Pitagorasz-tétel
20. Geometriai transzformációk
Térgeometria (testek)
21. Hasábok
22. Hengerek (NAT 2020-on túlmutató tananyag)
23. Gúlák (NAT 2020-on túlmutató tananyag)
24. Kúpok (NAT 2020-on túlmutató tananyag)
25. Gömb (NAT 2020-on túlmutató tananyag)
Függvények
26. Függvények, transzformációik, típusaik
27. Gyakorló videó, tesztek
Sorozatok (NAT 2020-on túlmutató tananyag)
28. A sorozat, mint függvény, számtani és mértani sorozatok
Nem találod amit keresel?

Garantáltan jól sikerülnek a DOLGOZATAID végig 8. osztályban. Egyszerű, érthető, vidám matek :)
Erőlködés és görcsök nélkül tanulhatod a matekot, és végre mindent érteni fogsz! Mindezt úgy, hogy még unatkoznod sem kell a matektanulás közben. B. Békési Bea
A szerethető matektanulás szakértője
Matektanár
Startolj jól a középiskolában!
Az általánost lassan befejezed, ezért Neked már a középiskolára érdemes összpontosítani! Mit tehetsz egy jó kezdésért? A Matek Oázis videókkal- Pótolhatod az esetleges korábbi hiányosságaidat
- a teljes 8.-os matekot meg tudod tanulni könnyen, érthetően.
- Emiatt garantáltan jól sikerülnek a DOLGOZATAID végig 8. osztályban.
- Ezért sok pontod lesz, és így felvesznek az áhított suliba.
- Ha akarod, a Felvételi felkészülésben is tudunk segíteni
(Másik oldalon találod)
Egyszerű, érthető, vidám matek :)
Erőlködés és görcsök nélkül tanulhatod a matekot, és végre mindent érteni fogsz! Mindezt úgy, hogy még unatkoznod sem kell a matektanulás közben.FONTOS! A kérdéseken gondolkozz el, és írd be, kattints rá, válaszd ki a megoldást! Szóval válaszolj légyszi a kérdésekre, mert csak így tudod elérni azt az eredményt, amit szeretnél!

A matek videók nagyon jók sokat használ.Végre matek órán nem csak a kosz ragad rám. Most már értem a matekot(vagyis kezdem érteni)
Mimi (8. oszt.) Diák
"A videók nagyon sokat segítettek, tavaly a videók segítségével lettem jó matekos, és idén is sokat segített! Nagyon köszönöm"
Végh Vanessza Szülő (v. nagyszülő)
Hálásan köszönet a világmegváltó kezdeményezésért, Melánia
Ördög Melánia
Sokszor nem fűlik hozzá a fogam és nem szeretek matekozni, azt viszont be kell látnom, hogy sokat segít a jegyem fenntartásában, és a felvételire való felkészülésben is nagy hasznomra volt.
Balázs Zalán Szülő (v. nagyszülő)Szeretnéd, ha gyermeked nem csak a matekban, hanem az élet minden területén sikeresebb lenne?
LOGIKA kurzusunk játékos és interaktív módon segít gyermekednek fejleszteni a kritikus gondolkodását és a problémamegoldó képességét, amelyek egy életre szóló előnyt jelentenek.